Seminario 8
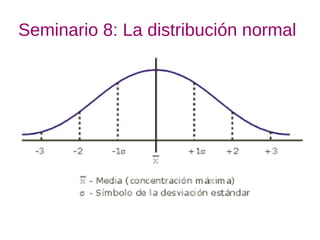
- 1. Seminario 8: La distribución normal
- 3. ¿Cuál es la probabilidad de que una destinataria de asistencia seleccionada al azar obtenga una puntuación de 10.5 o menos en la escala de autoestima? ● Lo primero que debemos hacer es tipificar el valor de 10'5 mediante la fórmula. Tipificar los valores nos sirve para compararlos con la curva normal. ● La fórmula que usamos es la de: donde Zx es el valor que vamos a mirar en las tablas de normalidad, X es el valor que queremos tipificar (en nuestro caso 10'5) el cual se le resta a la media (8) y esto se divide entre la desviación tipica (2) ● Esto quedaría como Zx= (10'5-8)/2= 2'5/2= 1'25 X X X X Z S − =
- 4. Tabla de normalidad. ● En la columna A miramos el valor de Z sea positivo o negatico. En nuestro caso es 1'25. ● Para saber cual de los dos valores elegir tenemos que saber qué es lo que buscamos. Nosotros queremos conocer la probabilidad de que una destinataria escogida al azar tenga una puntuación de 10'5 o menos en la escala de autoestima. ● Por tanto miramos el valor que se encuentra en la columna A que nos da el valor tipificado para los valores a la izquierda de la media. ● Sería 0'3944.
- 5. Resultados y Conclusiones ● Ya sabemos el conjunto de datos que hay entre 10'5 y 8. Tenemos que saber los que hay de 0 a 8, hasta la media. ● Sería un 0'5% de datos. ● Lo que hacemos es sumar: 0'3944+0'5= 0'8944 ● Lo podemos pasar a porcentajes y diremos que habría un 89'44% de probabilidad de que una mujer escogida al azar tuviera una puntuación de 10'5 o menos.
- 7. 1-¿Qué porcentaje de niños tienen una talla menor de 150 cm? ● Tipificamos el valor de 150 cm mediante la fórmula antes vista. ● Zx= (150-140)/5=2 ● Buscamos el valor de 2 en la tabla normal ● Tenemos que escoger 0'4772 para saber el conjunto de datos entre 150 cm y 140 cm. ● Tenemos que volver a sumar 0'5 para contemplar los valores que hay de 0 a 140 cm ya que nos pide el porcentaje de niños con una talla menor de 150 cm ● Sería entonces: 50%+ 47’72%=97’72% de los niños medirán menos de 150 cm
- 8. 2-¿Qué porcentaje de niños tienen una talla por encima de 150 cm? -Con el valor ya tipificado del apartado anterior solo debemos mirar el rango que corresponde a la derecha de la curva normal. Se agruparía un porcentaje de 0’0228 o lo que es lo mismo 2’28%. -También podemos hacerlo restando al 100% el valor anterior de 97’72%
- 9. 3-¿Cuál es el porcentaje de niños con una talla comprendida entre 137’25 y 145’50 cm? ● Tipificamos ambos valores a través de la fórmula: Zx= (137'25-140)/5= -0'552 Zx= (145'50-140)/5= 1'1 ● Buscamos estos valores en las tablas:
- 10. Resultados y conclusiones ● Escogeremos en ambos casos el valor más a la izquierda, es decir, el 0'2088 y el 0'3643. ● Sumamos ambos valores 0'2088+0'3644= 0'5731 ● Este resultado es el porcentaje de datos (57'31%) que se encuentran en el rango entre 137'25 cm y 145'50 cm.
- 12. 1 .Calcular la proporción de diabéticos con glucemia basal inferior o igual a 120. ● Tipificamos el valor de 120 mediante la fórmula Z= (120-106)/8= 1'75 ● Buscamos este valor en las tablas de normalidad. ● Escogemos el valor de más a la izquierda porque buscamos los datos menores de 120, es decir, elegimos 0'4599. Este es el conjunto de valores que hay entre 106 y 120. ● Debemos contemplar también desde 0 a 106. ● Sumamos por tanto → 0'4599+0'5= 0'9599 ● Diremos que la proporción de diabéticos con glucemia basal inferior o igual de 120 será de 95'99%
- 13. 2-La proporción de diabéticos con una glucemia basal comprendida entre 106 y 110 mg por ml ● Tipificamos el valor de 110 mg/ml mediante la fórmula de: Zx= (110-106)/8=0’5 Buscamos este valor en las tablas de normalidad de nuevo. ● Cogemos el valor de B donde los valores están más a la izquierda para saber qué porcentaje hay entre 106 y 110, serían un 19'15%
- 14. 3-La proporción de diabéticos con una glucemia basal mayor de 120 mg por 100 ml. Esto es el inverso del apartado 1. Por lo que al 100% de los datos le debemos restar 95’99% y el resultado será el 4’01% de los datos. 4. El nivel de glucemia basal tal que por debajo de él están el 25% de los diabéticos, es decir, le primer cuartil. ● Lo primero que tenemos que hacer es mirar el valor de 0'25 en la tabla de normalidad pero no en valor de Zx sino en la columna de A o de B.
- 15. ● Tenemos que calcular el valor de Z ya que no tenemos un valor concreto de 0'25. Hacemos la media ● (0'67+0'68)/2= 0'675 ● Sustituimos este valor fórmula ● 0'675= (X-106)/8 ● Despejamos obtenemos que el valor del primer cuartil es el de 111'4.