El documento trata sobre el movimiento armónico simple. Explica conceptos como amplitud, periodo, frecuencia, energía potencial y cinética en un oscilador armónico. Presenta varios ejemplos numéricos de problemas relacionados con osciladores armónicos simples y complejos como resortes, péndulos y sistemas masa-resorte.

1. MOVIMIENTO ARMÓNICO SIMPLE

2. Movimiento Armónico Simple

3. Movimiento Armónico Simple

4. Movimiento Armónico Simple

5. Movimiento Armónico Simple

6. Movimiento Armónico Simple

7. Movimiento Armónico Simple

8. Movimiento Armónico Simple

9. Movimiento Armónico Simple

10. Movimiento Armónico Simple

11. Movimiento Armónico Simple

12. Movimiento Armónico Simple

13. Movimiento Armónico Simple

14. Movimiento Armónico Simple

15. Movimiento Armónico Simple

16. Movimiento Armónico Simple

17. Movimiento Armónico Simple

18. MAS y Movimiento Circular

19. Energía del MAS

20. Energía del MAS

21. Energía del MAS

22. Energía del MAS
• Gráfica de E, K y U contra desplazamiento en un
MAS.

23. Ejemplo 01
Si un objeto en una superficie horizontal sin fricción
se une a un resorte, se desplaza y después se
suelta, oscilará. Si se desplaza 0.120 m de su
posición de equilibrio y se suelta con rapidez inicial
cero, después de 0.800 s su desplazamiento es de
0.120 m en el lado opuesto, habiendo pasado la
posición de equilibrio una vez durante este
intervalo. Calcule
a) la amplitud
b) el periodo
c) la frecuencia.

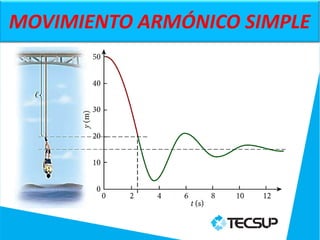
24. En la figura se muestra el desplazamiento de un
objeto oscilante en función del tiempo. Calcule a)
la frecuencia, b) la amplitud, c) el periodo y d) la
frecuencia angular de este movimiento.
Ejemplo 02

25. Un bloque de 2.00 kg, que se desliza sin fricción, se
conecta a un resorte ideal con constante de fuerza
de 300 N/m. En t = 0, el resorte no está estirado ni
comprimido, y el bloque se mueve en la dirección
negativa a 12.0 m/s. Calcule
a) la amplitud y
b) el ángulo de fase.
c) Escriba una ecuación para la posición en función
del tiempo.
Ejemplo 03

26. El desplazamiento en función del tiempo de una
masa de 1.50 kg en un resorte está dado por la
ecuación
𝑥𝑥 𝑡𝑡 = 7.40 𝑐𝑐𝑐𝑐 cos[ 4.16 𝑠𝑠−1
𝑡𝑡 − 2.42]
Calcule a) el tiempo que tarda una vibración
completa; b) la constante de fuerza del resorte; c) la
rapidez máxima de la masa; d) la fuerza máxima que
actúa sobre la masa; e) la posición, rapidez y
aceleración de la masa en t = 1.00 s; f ) y la fuerza
que actúa sobre la masa en ese momento.
Ejemplo 04

27. Dentro de un vehículo de prueba de la NASA, se tira de
una esfera de 3.50 kg mediante un resorte ideal
horizontal que está unido a una mesa sin fricción. La
constante de fuerza del resorte es de 225 N/m. El
vehículo tiene una aceleración constante de 5.00 𝑚𝑚/𝑠𝑠2
,
y la esfera no oscila. De repente, cuando la rapidez del
vehículo llega a 45.0 m/s, sus motores se apagan,
eliminando así su aceleración pero no su velocidad.
Calcule a) la amplitud y b) la frecuencia de las
oscilaciones resultantes de la esfera. c) ¿Cuál será la
rapidez máxima de la esfera en relación con el
vehículo?
Ejemplo 05

28. Péndulo simple
Sistema
realizado en
el
Laboratorio

29. Péndulo simple

30. Péndulo simple

31. Péndulo simple

32. Péndulo simple

33. Se tira de un péndulo simple de 0.240 m de
longitud para moverlo 3.50° a un lado y luego se
suelta. a) ¿Cuánto tarda la lenteja del péndulo en
alcanzar su rapidez máxima? b) ¿Cuánto tarda si el
ángulo es de 1.75° en vez de 3.50°?
Ejemplo 06

34. Un péndulo simple de 3,00 m de largo oscila con
un desplazamiento angular máximo de 0,4 rad.
a) Calcule su rapidez lineal v en su punto más bajo.
b) Calcule su aceleración lineal a en los extremos
de su movimiento.
Ejemplo 07

35. Una manzana pesa 1N. si la colgamos del extremo
de un resorte largo con k = 2 N/m y masa
insignificante, rebota verticalmente con un MAS. Si
tenemos el rebote y dejamos que la manzana oscile
de lado a lado con un ángulo pequeño, la
frecuencia de este movimiento es la mitad de la del
movimiento de rebote. ¿Qué longitud tiene el
resorte no estirado?
Ejemplo 08

36. Péndulo físico

37. Péndulo físico

38. Una llave inglesa de 1,5 kg pivota en un extremo y
oscila como un péndulo físico. El periodo para
oscilaciones de ángulo pequeño es de 0,82 s, y el
pivote esta a 0,3 m del centro de masa.
a) ¿Qué momento de inercia tiene la llave respecto
a un eje que pasa por el pivote?
b) Si la llave inicialmente se desplaza 0,6 rad de la
posición de equilibrio, ¿Qué velocidad angular
tiene al pasar por dicha posición?
Ejemplo 09

39. Un adorno navideño con forma de esfera sólida de
masa M = 0,015 kg y radio R = 0,05 m se cuelga de
una rama un trozo de alambre unido a la superficie
de la esfera. Si el adorno se desplaza una distancia
corta y se suelta, oscila como un péndulo físico.
Calcule su periodo (Ignore la fricción en el pivote. EL
momento de inercia de esfera respecto al pivote en
la rama es
7
5
𝑀𝑀𝑅𝑅2
)
Ejemplo 10

40. Sistemas oscilantes: muelle vertical

41. Sistemas oscilantes: muelle vertical

42. Sistemas oscilantes: muelle vertical

43. Sistemas oscilantes: muelle vertical

44. Un orgulloso pescador de alta mar cuelga un pez de
65.0 kg de un resorte ideal con masa despreciable,
estirando el resorte 0.120 m. a) Calcule la constante
de fuerza del resorte. Ahora se tira del pez 5.00 cm
hacia abajo y luego se suelta. b) ¿Qué periodo de
oscilación tiene el pez? c) ¿Qué rapidez máxima
alcanzará?
Ejemplo 11

45. Un oscilador consiste de un bloque sujetado a un
resorte (k=400 N/m). En algún tiempo (medido
desde la posición de equilibrio), velocidad y
aceleración del bloque son: x=0.100m, v=-13.6m/s y
a=-123 𝑚𝑚/𝑠𝑠2
. Calcular:
(a) La frecuencia de oscilación.
(b)La masa del bloque.
(c) La amplitud del movimiento.
Problema01

46. Un oscilador armónico consiste de un bloque de
masa de 2.00 kg sujetado a un resorte de constante
100 N/m. Cuando t=1.00 s, la posición y la velocidad
del bloque es x=0.129m y v=3.415m/s.
(a) ¿Cuál es la amplitud de la oscilación?
(b)La posición y la velocidad del bloque en t=0s.
Problema02

47. En la figura posición vs. Tiempo la gráfica de una
partícula en movimiento armónico simple.
(a) ¿Cuál es la constante de fase?
(b)¿Cuál es la velocidad en t=0s?
(c) ¿Cuál es la velocidad máxima?
Problema03

48. La figura muestra la velocidad vs. Tiempo de una
partícula en movimiento armónico simple.
(a) ¿Cuál es la amplitud de la oscilación?
(b)¿Cuál es la constante de fase?
(c) ¿Cuál es la posición en t=0s?
Problema04

49. Las dos gráficas de la figura son de dos sistemas masa-resorte vertical.
(a) ¿Cuál es la frecuencia del sistema A? ¿Cuál es el primer tiempo en el
cual la masa tiene la máxima velocidad mientras viaja en la dirección
hacia arriba?
(b) ¿Cuál es el periodo del sistema B? ¿Cuál es el primer tiempo en el cual
la energía es solo potencial?
(c) Si ambos sistemas tienen las mismas masas, cual es la razón 𝑘𝑘𝐴𝐴/𝑘𝑘𝐵𝐵 de
las constantes de los resortes?
Problema05

50. Un bloque está sobre un émbolo que se mueve
verticalmente con movimiento armónico simple.
(a) ¿A qué amplitud del movimiento se separarán el
bloque y el émbolo si el periodo del movimiento
del émbolo es de 1.18 s?
(b)Si el émbolo tiene una amplitud de 5.12 cm en su
movimiento, halle la frecuencia máxima a la cual
estarán en contacto el bloque y el émbolo
continuamente.
Problema06

51. (a) Cuando el desplazamiento es la mitad de la
amplitud ¿qué fracción de la energía total es
cinética y que fracción es potencial en el
movimiento armónico simple?
(b)¿A qué desplazamiento es la energía mitad
cinética y mitad potencial?
Problema07

52. Una partícula de 12.3 kg se halla en movimiento
armónico simple con una amplitud de 1.86 mm. La
aceleración máxima de la partícula es de 7.93
km/𝑠𝑠2
.
(a) Halle el periodo del movimiento.
(b)¿Cuál es la velocidad máxima de la partícula?
(c) Calcule la energía mecánica total de este
oscilador armónico simple.
Problema08

53. Un objeto de 5.13 kg se mueve sobre una superficie
horizontal sin fricción bajo la influencia de un
resorte de constante de fuerza 9.88 N/cm. El objeto
es desplazado 53.5 cm y se le da una velocidad
inicial de 11.2 m/s hacia la posición de equilibrio.
Halle:
(a) La frecuencia del movimiento
(b)La energía potencial inicial del sistema
(c) La energía cinética inicial
(d)La amplitud del movimiento.
Problema09