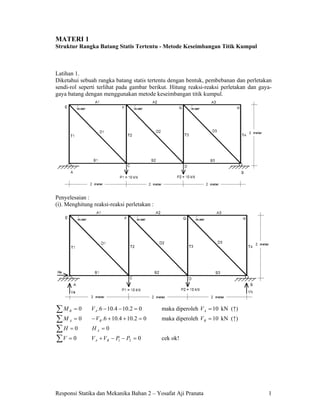
titik buhul dan cremona
- 1. MATERI 1 Struktur Rangka Batang Statis Tertentu - Metode Keseimbangan Titik Kumpul Latihan 1. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang dengan menggunakan metode keseimbangan titik kumpul. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan : ∑M = 0 B V A .6 − 10.4 − 10.2 = 0 maka diperoleh V A = 10 kN (↑) ∑M = 0A − V B .6 + 10.4 + 10.2 = 0 maka diperoleh V B = 10 kN (↑) ∑H = 0 HA = 0 ∑V = 0 V A + V B − P1 − P2 = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 1
- 2. (ii). Menghitung gaya-gaya batang : Titik A. ∑V = 0 V A + T1 = 0 T1 = −10 kN (batang tekan) ∑H = 0 B1 = 0 (batang B1 tidak ada gaya) Titik E. ∑V = 0 − T1 − D1 . sin 45 o = 0 D1 = 14,1421 kN (batang tarik) ∑H = 0 D1 . cos 45 o + A1 = 0 A1 = −10 kN (batang tekan) Titik C. ∑H = 0 − B1 − D1 . cos 45 o + B2 = 0 − B1 − 14,1421. cos 45 o + B2 = 0 B2 = 10 kN (batang tarik) ∑V = 0 − P1 + D1 . sin 45 o + T2 = 0 − 10 + 14,1421. sin 45 o + T2 = 0 T2 = 0 (batang T2 tidak ada gaya) Titik F. ∑V = 0 − D2 . sin 45 o − T2 = 0 D2 = 0 (batang D2 tidak ada gaya) ∑H = 0 − A1 + D2 . cos 45 o + A2 = 0 − (− 10) + (0 ). cos 45o + A2 = 0 A2 = −10 kN (batang tekan) Titik D. ∑H = 0 − B2 − D2 . cos 45 o + B3 = 0 − 10 − (0 ). cos 45 o + B3 = 0 B3 = 10 kN (batang tarik) ∑V = 0 − P2 + D2 . sin 45 o + T3 = 0 − 10 + (0 ). sin 45 o + T3 = 0 T3 = 10 kN (batang tarik) Titik G. ∑H = 0 − T3 − D3 . cos 45 o = 0 − 10 − D3 . cos 45 o = 0 D3 = −14,1421 kN (batang tekan) ∑V = 0 − A2 + D3 . sin 45 o + A3 = 0 − (− 10 ) + (− 14,1421). sin 45 o + A3 = 0 A3 = 0 (batang A3 tidak ada gaya) Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 2
- 3. Titik B. ∑V = 0 VB + D3 . sin 45 o + T4 = 0 10 + (− 14,1421). sin 45 o + T4 = 0 T4 = 0 (batang T4 tidak ada gaya) ∑H = 0 − B3 − D3 . cos 45 o = 0 − 10 − (− 14,1421). cos 45 o = 0 ok! Titik H. dari hasil perhitungan sebelumnya telah diperoleh, A3 = 0 (batang A3 tidak ada gaya) T4 = 0 (batang T4 tidak ada gaya) Hasil gaya-gaya batang secara keseluruhan dapat ditampilkan dalam tabel sebagai berikut, batang gaya (kN) keterangan A1 10 batang tekan A2 10 batang tekan A3 0 - T1 10 batang tekan T2 0 - T3 10 batang tarik T4 0 - D1 14,1421 batang tarik D2 0 - D3 14,1421 batang tekan B1 0 - B2 10 batang tarik B3 10 batang tarik Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 3
- 4. Latihan 2. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang dengan menggunakan metode keseimbangan titik kumpul. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan : ∑V = 0 V A − P1 − P2 = 0 maka diperoleh V A = 20 kN (↑) ∑M = 0 H − H A .2 + V A .6 − 10.4 − 10.2 = 0 maka diperoleh H A = 30 kN (→) ∑M = 0A − H H .2 + 10.4 + 10.2 = 0 maka diperoleh H H = 30 kN (←) ∑H = 0 HA − HH = 0 cek ok! (ii). Menghitung gaya-gaya batang : Titik A. ∑V = 0 V A + T1 = 0 T1 = −20 kN (batang tekan) ∑H = 0 H A + B1 = 0 B1 = −30 kN (batang tekan) Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 4
- 5. Titik E. ∑V = 0 − T1 − D1 . sin 45 o = 0 D1 = 28,2842 kN (batang tarik) ∑H = 0 D1 . cos 45 o + A1 = 0 A1 = −20 kN (batang tekan) Titik C. ∑H = 0 − B1 − D1 . cos 45 o + B2 = 0 − B1 − 28,2842. cos 45 o + B2 = 0 B2 = −10 kN (batang tekan) ∑V = 0 − P1 + D1 . sin 45 o + T2 = 0 − 10 + 28,2842. sin 45 o + T2 = 0 T2 = −10 kN (batang tekan) Titik F. ∑V = 0 − D2 . sin 45 o − T2 = 0 − D2 . sin 45 o − (− 10 ) = 0 D2 = 14,1421 kN (batang tarik) ∑H = 0 − A1 + D2 . cos 45 o + A2 = 0 − (− 20) + (14,1421). cos 45 o + A2 = 0 A2 = −30 kN (batang tekan) Titik D. ∑H = 0 − B2 − D2 . cos 45 o + B3 = 0 − (− 10) − (14,1421). cos 45 o + B3 = 0 B3 = 0 (batang A3 tidak ada gaya) ∑V = 0 − P2 + D2 . sin 45 o + T3 = 0 − 10 + (14,1421). sin 45 o + T3 = 0 T3 = 0 (batang T3 tidak ada gaya) Titik G. ∑H = 0 − T3 − D3 . cos 45 o = 0 − 0 − D3 . cos 45 o = 0 D3 = 0 (batang D 3 tidak ada gaya) ∑V = 0 − A2 + D3 . sin 45 o + A3 = 0 − (− 30) + (0). sin 45 o + A3 = 0 A3 = −30 kN (batang tekan) Titik B. ∑V = 0 D3 . sin 45 o + T4 = 0 (0). sin 45 o + T4 = 0 T4 = 0 (batang T4 tidak ada gaya) ∑H = 0 − B3 − D3 . cos 45 o = 0 − 0 − (0). cos 45 o = 0 ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 5
- 6. Titik H. dari hasil perhitungan sebelumnya telah diperoleh, A3 = −30 kN (batang tekan) T4 = 0 (batang T4 tidak ada gaya) Hasil gaya-gaya batang secara keseluruhan dapat ditampilkan dalam tabel sebagai berikut, batang gaya (kN) keterangan A1 20 batang tekan A2 30 batang tekan A3 30 batang tekan T1 20 batang tekan T2 10 batang tekan T3 0 - T4 0 - D1 28,2842 batang tarik D2 14,1421 batang tarik D3 0 - B1 30 batang tekan B2 10 batang tekan B3 0 - Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 6
- 7. Latihan 3. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang dengan menggunakan metode keseimbangan titik kumpul. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan : ∑V = 0 V A − P1 − P2 − P3 − P4 = 0 maka diperoleh V A = 80 kN (↑) ∑M B =0 H A .2 + P4 .8 + P3 .8 + P2 .6 + P1 .4 = 0 H A .2 + 20.8 + 20.8 + 20.6 + 20.4 = 0 maka diperoleh H A = −260 kN (←) ∑M A =0 − H B .2 − VB .0 + P4 .8 + P3 .8 + P2 .6 + P1 .4 = 0 − H B .2 − V B .0 + 20.8 + 20.8 + 20.6 + 20.4 = 0 maka diperoleh H B = 260 kN (→) ∑H = 0 HA + HB = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 7
- 8. (ii). Menghitung gaya-gaya batang : Titik B. ∑V = 0 VB + T1 = 0 T1 = −80 kN (batang tekan) ∑H = 0 H B + B1 = 0 B1 = −260 kN (batang tekan) Titik A. ∑V = 0 − T1 − D1 . sin 45 o = 0 D1 = 113,14 kN (batang tarik) ∑H = 0 H A + D1 . cos 45 o + A1 = 0 A1 = 180 kN (batang tarik) Titik C. ∑H = 0 − B1 − D1 . cos 45 o + B2 = 0 − B1 − 113,14. cos 45 o + B2 = 0 B2 = −180 kN (batang tekan) ∑V = 0 D1 . sin 45 o + T2 = 0 113,14. sin 45 o + T2 = 0 T2 = −80 kN (batang tekan) Titik D. ∑V = 0 − D2 . sin 45 o − T2 = 0 − D2 . sin 45 o − (− 80 ) = 0 D2 = 113,14 kN (batang tarik) ∑H = 0 − A1 + D2 . cos 45 o + A2 = 0 − (180) + (113,14). cos 45 o + A2 = 0 A2 = 100 kN (batang tarik) Titik E. ∑H = 0 − B2 − D2 . cos 45 o + B3 = 0 − (− 180) − (113,14). cos 45 o + B3 = 0 B3 = −100 kN (batang tekan) ∑V = 0 − P1 + D2 . sin 45 o + T3 = 0 − 20 + (113,14). sin 45 o + T3 = 0 T3 = −60 kN (batang tekan) Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 8
- 9. Titik F. ∑H = 0 − T3 − D3 . cos 45 o = 0 − (− 60) − D3 . cos 45 o = 0 D3 = 84,85 kN (batang tarik) ∑V = 0 − A2 + D3 . sin 45 o + A3 = 0 − (100) + 84,85. sin 45 o + A3 = 0 A3 = 40 kN (batang tarik) Titik G. ∑V = 0 D3 . sin 45 o + T4 − 20 = 0 (84,85). sin 45 o + T4 − 20 = 0 T4 = −40 kN (batang tekan) ∑H = 0 − B3 − D3 . cos 45 o + B4 = 0 − (− 100 ) − (84,85). cos 45 o + B4 = 0 B4 = −40 kN (batang tekan) Titik H. ∑V = 0 D4 . sin 45 o + T4 = 0 D4 . sin 45 o + (− 40) = 0 D4 = 56,57 (batang tarik) ∑H = 0 − A3 + A4 + D4 . cos 45 o = 0 A4 = 0 (batang A4 tidak ada gaya) Titik I. ∑V = 0 − P3 + D4 . sin 45 o + T5 = 0 − 20 + (56,57 ). sin 45 o + T5 = 0 T5 = −20 kN (batang tekan) ∑H = 0 − B4 − D4 . cos 45 o = 0 − (− 40) − (56,57 ). cos 45 o = 0 ok! Titik J. dari hasil perhitungan sebelumnya telah diperoleh, ∑H = 0 A4 = 0 (batang A4 tidak ada gaya) ok! ∑V = 0 − P4 + T5 = 0 T5 = −20 kN (batang tekan) ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 9
- 10. Hasil gaya-gaya batang secara keseluruhan dapat ditampilkan dalam tabel sebagai berikut, batang gaya (kN) keterangan A1 180 batang tarik A2 100 batang tarik A3 40 batang tarik A4 0 - T1 80 batang tekan T2 80 batang tekan T3 60 batang tekan T4 40 batang tekan T5 20 batang tekan D1 113,14 batang tarik D2 113,14 batang tarik D3 84,85 batang tarik D4 56,57 batang tarik B1 260 batang tekan B2 180 batang tekan B3 100 batang tekan B4 40 batang tekan Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 10
- 11. Latihan 4. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang dengan menggunakan metode keseimbangan titik kumpul. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan : ∑M B =0 V A .6 − 10.5 − 10.4 − 10.3 − 10.2 − 10.1 = 0 maka diperoleh V A = 25 kN (↑) ∑M A =0 − VB .6 + 10.1 + 10.2 + 10.3 + 10.4 + 10.5 = 0 maka diperoleh VB = 25 kN (↑) ∑H = 0 HA = 0 ∑V = 0 V A + VB − 10 − 10 − 10 − 10 − 10 = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 11
- 12. (ii). Menghitung gaya-gaya batang : Karena model struktur rangka pada kasus ini berbentuk simetris, maka untuk menghitung gaya-gaya batang cukup kita tinjau titik A, titik C, titik D dan titik E. Titik A. ∑V = 0 D1 . sin 45 o + V A = 0 D1 . sin 45 o + 25 = 0 D1 = −35,36 kN (batang tekan) ∑H = 0 B1 + D1 . cos 45 o = 0 B1 + (− 35,36). sin 45 o = 0 B1 = 25 kN (batang tarik) Titik C. ∑V = 0 − D1 . sin 45 o − D2 . sin 45 o − P + D3 . sin 26,565 o = 0 − (− 35,36). sin 45 o − D2 . sin 45 o − 10 + D3 . sin 26,565 o = 0 − 0,707.D2 + 0,447.D3 = −15 …….…. (1) ∑H = 0 − D1 . cos 45 o + D2 . cos 45 o + D3 . cos 26,565 o = 0 − (− 35,36). cos 45 o + D2 . cos 45 o + D3 . cos 26,565 o = 0 0,707.D2 + 0,894.D3 = −25 ……….. (2) dari persamaan (1) dan (2) dapat kita peroleh, D2 = 2,357 kN (batang tarik) D3 = −29,828 kN (batang tekan) Titik D. ∑V = 0 − P + D2 . sin 45 o + D4 . sin 63,435 o = 0 − 10 + 2,357. sin 45 o + D4 . sin 63,435 o = 0 D4 = 9,316 kN (batang tarik) ∑H = 0 − B1 − D2 . cos 45 o + D4 . cos 63,435 o + B2 = 0 − 25 − 2,357. cos 45 o + 9,316. cos 63,435 o + B2 = 0 B2 = 22,5 kN (batang tarik) Titik E. ∑V = 0 − P − D3 . sin 26,565 o − D4 . sin 63,435 o − D6 . sin 26,565 o − D5 . sin 63,435 o = 0 − 10 − (− 29,828). sin 26,565 o − 9,316. sin 63,435 o − D6 . sin 26,565 o − D5 . sin 63,435 o = 0 − 0,894 D5 − 0,447.D6 = 5 …….…. (3) Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 12
- 13. ∑H = 0 − D3 . cos 26,565 o − D4 . cos 63,435 o + D6 . cos 26,565 o + D5 . cos 63,435 o = 0 − (− 29,828). cos 26,565 o − 9,316. cos 63,435 o + D6 . cos 26,565 o + D5 . cos 63,435 o = 0 0,447 D5 + 0,894.D6 = −22,513 ……….. (4) dari persamaan (3) dan (4) dapat kita peroleh, D5 = 9,316 kN (batang tarik) D6 = −29,828 kN (batang tekan) Karena bentuk stuktur rangka adalah simetris, maka dapat kita hitung, D7 = D2 = 2,357 kN (batang tarik) D8 = D1 = −35,36 kN (batang tekan) B3 = B1 = 25 kN (batang tarik) Hasil gaya-gaya batang secara keseluruhan dapat ditampilkan dalam tabel sebagai berikut, batang gaya (kN) keterangan B1 25 batang tarik B2 22,5 batang tarik B3 25 batang tarik D1 35,36 batang tekan D2 2,357 batang tarik D3 29,828 batang tekan D4 9,316 batang tarik D5 9,316 batang tarik D6 29,828 batang tekan D7 2,357 batang tarik D8 35,36 batang tekan Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 13
- 14. TUGAS 1 Diketahui : Sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Ditanyakan : Hitung reaksi-reaksi perletakan dan gaya-gaya batang dengan menggunakan metode keseimbangan titik kumpul. Tugas dikumpulkan paling lambat dua minggu terhitung sejak soal tugas diberikan kepada mahasiswa. ----- Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 14
- 15. MATERI 2 Struktur Rangka Batang Statis Tertentu - Metode Potongan Latihan 1. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang A1, D1, B1, A2, T3 dan B3 dengan menggunakan metode potongan. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan : ∑M = 0 B V A .6 − 10.4 − 10.2 = 0 maka diperoleh V A = 10 kN (↑) ∑M = 0A − VB .6 + 10.4 + 10.2 = 0 maka diperoleh V B = 10 kN (↑) ∑H = 0 HA = 0 ∑V = 0 V A + V B − P1 − P2 = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 15
- 16. (ii). Menghitung gaya-gaya batang pada potongan 1-1: ∑ M E = 0 − B1 .2 = 0 B1 = 0 (batang B1 tidak ada gaya) ∑V = 0 V A − D1 . sin 45 o = 0 10 − D1 . sin 45 o = 0 D1 = 14,1421 kN (batang tarik) ∑H = 0 A1 + D1 . cos 45 o + B1 = 0 A1 = −10 kN (batang tekan) (iii). Menghitung gaya-gaya batang pada potongan 2-2: ∑V = 0 V A − P1 − P2 + T3 = 0 10 − 10 − 10 + T3 = 0 T3 = 10 kN (batang tarik) ∑M D =0 V A .4 + A2 .2 − P1 .2 = 0 10.4 + A2 .2 − 10.2 = 0 A2 = −10 kN (batang tekan) ∑H = 0 A2 + B3 = 0 B3 = 10 kN (batang tarik) Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 16
- 17. Latihan 2. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang A1, T2 dan B2 dengan menggunakan metode potongan. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan : ∑V = 0 V A − P1 − P2 = 0 maka diperoleh V A = 20 kN (↑) ∑M = 0 H − H A .2 + V A .6 − 10.4 − 10.2 = 0 maka diperoleh H A = 30 kN (→) ∑M = 0A − H H .2 + 10.4 + 10.2 = 0 maka diperoleh H H = 30 kN (←) ∑H = 0 HA − HH = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 17
- 18. (ii). Menghitung gaya-gaya batang pada potongan 1-1: ∑V = 0 V A − P1 + T2 = 0 20 − 10 + T3 = 0 T2 = −10 kN (batang tekan) ∑M C =0 V A .2 + A1 .2 = 0 20.2 + A1 .2 = 0 A1 = −20 kN (batang tekan) ∑H = 0 A1 + B2 + H A = 0 B2 = −10 kN (batang tekan) Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 18
- 19. Latihan 3. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang A3, D3 dan B3 dengan menggunakan metode potongan. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan : ∑V = 0 VB − P1 − P2 − P3 − P4 = 0 maka diperoleh VB = 80 kN (↑) ∑M B =0 H A .2 + P4 .8 + P3 .8 + P2 .6 + P1 .4 = 0 H A .2 + 20.8 + 20.8 + 20.6 + 20.4 = 0 maka diperoleh H A = −260 kN (←) ∑M A =0 − H B .2 − VB .0 + P4 .8 + P3 .8 + P2 .6 + P1 .4 = 0 − H B .2 − V B .0 + 20.8 + 20.8 + 20.6 + 20.4 = 0 maka diperoleh H B = 260 kN (→) ∑H = 0 HA + HB = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 19
- 20. (ii). Menghitung gaya-gaya batang pada potongan 1-1 : ∑V = 0 VB − D2 . sin 45 o = 0 80 − D2 . sin 45 o = 0 D2 = 113,14 kN (batang tarik) ∑M C =0 − H B .2 + V B .2 − B 2 .2 = 0 − 260.2 + 80.2 − B 2 .2 = 0 B2 = −180 kN (batang tekan) ∑H = 0 H A + H B + A2 + D2 . cos 45 o + B2 = 0 − 260 + 260 + A2 + 113,14. cos 45 o + (− 180 ) = 0 A2 = 100 kN (batang tarik) Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 20
- 21. Latihan 4. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang D3, D4 dan B2 dengan menggunakan metode potongan. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan : ∑M B =0 V A .6 − 10.5 − 10.4 − 10.3 − 10.2 − 10.1 = 0 maka diperoleh V A = 25 kN (↑) ∑M A =0 − VB .6 + 10.1 + 10.2 + 10.3 + 10.4 + 10.5 = 0 maka diperoleh VB = 25 kN (↑) ∑H = 0 HA = 0 ∑V = 0 V A + VB − 10 − 10 − 10 − 10 − 10 = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 21
- 22. (ii). Menghitung gaya-gaya batang pada potongan 1-1 : ∑M D =0 V A .2 − P.1 + D 3 . sin 26,565 o .1 + D 3 . cos 26,565 o .1 = 0 25.2 − 10.1 + 1,341.D 3 = 0 D3 = −29,828 kN (batang tekan) ∑V = 0 V A − P − P + D 3 . sin 26,565 o + D 4 . sin 63,435 o = 0 25 − 10 − 10 + (− 29,828). sin 26,565 o + D 4 . sin 63,435 o = 0 D4 = 9,316 kN (batang tarik) ∑H = 0 D3 . cos 26,565 o + D4 . cos 63,435 o + B2 = 0 (− 29,828). cos 26,565o + 9,316. cos 63,435 o + B2 = 0 B2 = 22,5 kN (batang tarik) Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 22
- 23. TUGAS 2 Diketahui : Sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Ditanyakan : Hitung reaksi-reaksi perletakan dan gaya-gaya batang D2, T2, B2, D6, D7 dan B4 dengan menggunakan metode potongan. Tugas dikumpulkan paling lambat dua minggu terhitung sejak soal tugas diberikan kepada mahasiswa. ----- Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 23
- 24. MATERI 3 Struktur Rangka Batang Statis Tertentu - Metode Cremona Latihan 1. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang dengan menggunakan metode cremona. Penyelesaian : (i). menghitung reaksi-reaksi perletakan. ∑M c =0 V A .24 − P.16 = 0 V A = 66,6667 kN (↑) ∑M A =0 − VC .24 + P.8 = 0 VC = 33,3333 kN (↑) ∑H = 0 HA = 0 ∑V = 0 V A + VC − P = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 24
- 25. (ii). Penyelesaian diagram cremona. Batang Gaya Batang Keterangan (kN) D1 - 94,28 batang tekan D2 -74,54 batang tekan B1 66,67 batang tarik Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 25
- 26. Latihan 2. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang dengan menggunakan metode cremona. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan. ∑M c =0 V A .24 − P1 .18 − P2 .12 = 0 V A = 75 kN (↑) ∑M A =0 − VC .24 + P1 .6 + P2 .12 = 0 VC = 35 kN (↑) ∑H = 0 HA = 0 ∑V = 0 V A + VC − P = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 26
- 27. (ii). Penyelesaian diagram cremona. Batang Gaya Batang Keterangan (kN) A1 -52,5 batang tekan D1 -93,75 batang tekan D2 -6,25 batang tekan D3 +43,75 batang tarik D4 -43,75 batang tekan B1 +56,25 batang tarik B2 +26,25 batang tarik Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 27
- 28. Latihan 3. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang dengan menggunakan metode cremona. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan. ∑M c =0 V A .24 − P1 .18 − P2 .12 = 0 V A .24 − 80.18 − 30.12 = 0 V A = 75 kN (↑) ∑M A =0 − VC .24 − P2 .18 − P1 .12 = 0 − VC .24 − 30.18 − 80.12 = 0 VC = 35 kN (↑) ∑H = 0 HA = 0 ∑V = 0 V A + VC − P = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 28
- 29. (ii). Penyelesaian diagram cremona. Batang Gaya Batang Keterangan (kN) A1 -56,25 batang tekan A2 -26,25 batang tekan D1 -93,75 batang tekan D2 +6,25 batang tarik D3 -43,75 batang tekan D4 -43,75 batang tekan T1 -5 batang tekan T2 0 - T3 +35 batang tarik B1 +56,25 batang tarik B2 +52,5 batang tarik B3 +52,5 batang tarik B4 +26,25 batang tarik Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 29
- 30. Latihan 4. Diketahui sebuah rangka batang statis tertentu dengan bentuk, pembebanan dan perletakan sendi-rol seperti terlihat pada gambar berikut. Hitung reaksi-reaksi perletakan dan gaya- gaya batang dengan menggunakan metode cremona. Penyelesaian : (i). Menghitung reaksi-reaksi perletakan. ∑M B =0 V A .6 − P.3 + P.25 + P.25 = 0 V A .6 − 25.3 + 25.3 + 25.6 = 0 V A = −25 kN (↓) ∑M A =0 − V B .6 + P.3 + P.9 + P.12 = 0 − V B .6 + 25.3 + 25.9 + 25.12 = 0 V B = 100 kN (↑) ∑H = 0 HA = 0 ∑V = 0 V A + VB − P = 0 cek ok! Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 30
- 31. (ii). Penyelesaian diagram cremona. Batang Gaya Batang Keterangan (kN) D1 +55,90 batang tarik D2 -27,95 batang tekan D3 +83,85 batang tarik D4 +83,85 batang tarik D5 -27,95 batang tekan D6 +55,90 batang tarik T1 +25 batang tarik T2 -75 batang tekan T3 +25 batang tarik B1 -50 batang tekan B2 -50 batang tekan B3 -50 batang tekan B4 -50 batang tekan Responsi Statika dan Mekanika Bahan 2 – Yosafat Aji Pranata 31
