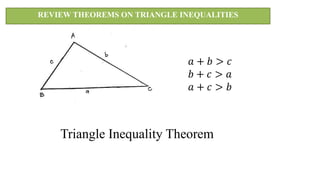
1. REVIEW THEOREMS ON TRIANGLE INEQUALITIES
𝑎 + 𝑏 > 𝑐
𝑏 + 𝑐 > 𝑎
𝑎 + 𝑐 > 𝑏
Triangle Inequality Theorem

2. REVIEW THEOREMS ON TRIANGLE INEQUALITIES
∠𝐵 > ∠𝐶
𝐴𝐶 > 𝐴𝐵
Angle-side Inequality Theorem

3. REVIEW THEOREMS ON TRIANGLE INEQUALITIES
𝐴𝐶 > 𝐵𝐶
∠𝐵 > ∠𝐴
Side-angle Inequality Theorem

4. REVIEW THEOREMS ON TRIANGLE INEQUALITIES
∠6 > ∠1
∠6 > ∠2
∠4 < ∠2
∠4 < ∠3
Exterior Angle Inequality Theorem

5. REVIEW THEOREMS ON TRIANGLE INEQUALITIES
𝐴𝐵 ≅ 𝐷𝐸
𝐸𝐹 ≅ 𝐵𝐶
∠𝐵 > ∠𝐸
𝐴𝐶 > 𝐷𝐹
Hinge Theorem

6. REVIEW THEOREMS ON TRIANGLE INEQUALITIES
𝐴𝐵 ≅ 𝐷𝐸
𝐸𝐹 ≅ 𝐵𝐶
∠𝐵 > ∠𝐸
𝐴𝐶 > 𝐷𝐹
Converse of Hinge Theorem

7. OBJECTIVES:
Learning Competency: Proves inequalities in a triangle.
M8GE-IVc-1
Learning Objectives:
1. Familiarize triangles inequality theorems.
2. Prove inequalities in a triangle.
3. Participate actively on class discussion.

8. EXAMPLE 1
Given:
𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾
m∠𝑈𝐾𝐶 > 𝑚∠𝐾𝑈𝐶
Prove:
𝑈𝐿 > 𝐶𝐾
Proof:
Statements Reasons
1
2.
3.

9. EXAMPLE 1
Given:
𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾
𝑀∠𝑈𝐾𝐶 > 𝑀∠𝐾𝑈𝐶
Prove:
𝑈𝐿 > 𝐶𝐾
Proof:
Statements Reasons
1. 𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾
2.
3.

10. EXAMPLE 1
Given:
𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾
𝑀∠𝑈𝐾𝐶 > 𝑀∠𝐾𝑈𝐶
Prove:
𝑈𝐿 > 𝐶𝐾
Proof:
Statements Reasons
1. 𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾 Given
2.
3.

11. EXAMPLE 1
Given:
𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾
𝑀∠𝑈𝐾𝐶 > 𝑀∠𝐾𝑈𝐶
Prove:
𝑈𝐿 > 𝐶𝐾
Proof:
Statements Reasons
1. 𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾 Given
2. 𝑚∠𝑈𝐾𝐶 > 𝑚∠𝐾𝑈𝐶
3.

12. EXAMPLE 1
Given:
𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾
𝑀∠𝑈𝐾𝐶 > 𝑀∠𝐾𝑈𝐶
Prove:
𝑈𝐿 > 𝐶𝐾
Proof:
Statements Reasons
1. 𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾 Given
2. 𝑚∠𝑈𝐾𝐶 > 𝑚∠𝐾𝑈𝐶 Given
3.

13. EXAMPLE 1
Given:
𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾
𝑀∠𝑈𝐾𝐶 > 𝑀∠𝐾𝑈𝐶
Prove:
𝑈𝐿 > 𝐶𝐾
Proof:
Statements Reasons
1. 𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾 Given
2. 𝑚∠𝑈𝐾𝐶 > 𝑚∠𝐾𝑈𝐶 Given
3. 𝑈𝐿 > 𝐶𝐾

14. EXAMPLE 1
Given:
𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾
𝑀∠𝑈𝐾𝐶 > 𝑀∠𝐾𝑈𝐶
Prove:
𝑈𝐿 > 𝐶𝐾
Proof:
Statements Reasons
1. 𝐿𝐶 ≅ 𝐶𝑈; 𝐶𝑈 ≅ 𝑈𝐾 Given
2. 𝑚∠𝑈𝐾𝐶 > 𝑚∠𝐾𝑈𝐶 Given
3. 𝑈𝐿 > 𝐶𝐾 Angle-side Inequality Theorem

15. EXAMPLE 2
Given:
𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿
Prove:
𝐶𝐼 > 𝐶𝑅
Proof:
Statements Reasons
1.
2.
3.

16. EXAMPLE 2
Given:
𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿
Prove:
𝐶𝐼 > 𝐶𝑅
Proof:
Statements Reasons
1. 𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿
2.
3.

17. EXAMPLE 2
Given:
𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿
Prove:
𝐶𝐼 > 𝐶𝑅
Proof:
Statements Reasons
1. 𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿 Given
2.
3.

18. EXAMPLE 2
Given:
𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿
Prove:
𝐶𝐼 > 𝐶𝑅
Proof:
Statements Reasons
1. 𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿 Given
2. 𝑚∠𝐶𝑅𝐼 > 𝑚∠𝐶𝐼𝑅
3.

19. EXAMPLE 2
Given:
𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿
Prove:
𝐶𝐼 > 𝐶𝑅
Proof:
Statements Reasons
1. 𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿 Given
2. 𝑚∠𝐶𝑅𝐼 > 𝑚∠𝐶𝐼𝑅 Side-angle Inequality Theorem
3.

20. EXAMPLE 2
Given:
𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿
Prove:
𝐶𝐼 > 𝐶𝑅
Proof:
Statements Reasons
1. 𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿 Given
2. 𝑚∠𝐶𝑅𝐼 > 𝑚∠𝐶𝐼𝑅 Side-angle Inequality Theorem
3. 𝐶𝐼 > 𝐶𝑅 Angle-side Inequality Theorem

21. EXAMPLE 2
Given:
𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿
Prove:
𝐶𝐼 > 𝐶𝑅
Proof:
Statements Reasons
1. 𝑌𝑅 ≅ 𝐿𝐼; 𝐼𝑌 > 𝑅𝐿 Given
2. 𝑚∠𝐶𝑅𝐼 > 𝑚∠𝐶𝐼𝑅 Side-angle Inequality Theorem
3. 𝐶𝐼 > 𝐶𝑅

22. EXAMPLE 3
Given:
𝐴𝐵 ≅ 𝐶𝐷; 𝐴𝐷 < 𝐵𝐶
Prove:
𝑚∠1 < 𝑚∠4
Proof:
Statement Reasons
1. Given
2. 𝐵𝐷 ≅ 𝐵𝐷
3. Given
4. 𝑚∠1 < 𝑚∠4

23. EXAMPLE 3
Given:
𝐴𝐵 ≅ 𝐶𝐷; 𝐵𝐶 < 𝐴𝐷
Prove:
𝑚∠1 < 𝑚∠4
Proof:
Statement Reasons
1. 𝐴𝐵 ≅ 𝐶𝐷 Given
2. 𝐵𝐷 ≅ 𝐵𝐷
3. Given
4. 𝑚∠1 < 𝑚∠4

24. EXAMPLE 3
Given:
𝐴𝐵 ≅ 𝐶𝐷; 𝐵𝐶 < 𝐴𝐷
Prove:
𝑚∠1 < 𝑚∠4
Proof:
Statement Reasons
1. 𝐴𝐵 ≅ 𝐶𝐷 Given
2. 𝐵𝐷 ≅ 𝐵𝐷 Reflexive
3. Given
4. 𝑚∠1 < 𝑚∠4

25. EXAMPLE 3
Given:
𝐴𝐵 ≅ 𝐶𝐷; 𝐴𝐷 < 𝐵𝐶
Prove:
𝑚∠1 < 𝑚∠4
Proof:
Statement Reasons
1. 𝐴𝐵 ≅ 𝐶𝐷 Given
2. 𝐵𝐷 ≅ 𝐵𝐷 Reflexive
3. 𝐴𝐷 < 𝐵𝐶 Given
4. 𝑚∠1 < 𝑚∠4

26. EXAMPLE 3
Given:
𝐴𝐵 ≅ 𝐶𝐷; 𝐵𝐶 < 𝐴𝐷
Prove:
𝑚∠1 < 𝑚∠4
Proof:
Statement Reasons
1. 𝐴𝐵 ≅ 𝐶𝐷 Given
2. 𝐵𝐷 ≅ 𝐵𝐷 Reflexive
3. A𝐷 < 𝐵𝐶 Given
4. 𝑚∠1 < 𝑚∠4 The Converse of the Hinge Theorem

27. EXAMPLE 4
Given:
∆𝐹𝑀𝐴; 𝐹𝐴 ≅ 𝑀𝑅
Prove:
𝐹𝑀 > 𝐴𝑅
Proof:
Statement Reasons
1.
2.
3.
4.

28. EXAMPLE 4
Given:
∆𝐹𝑀𝐴; 𝐹𝐴 ≅ 𝑀𝑅
Prove:
𝐹𝑀 > 𝐴𝑅
Proof:
Statements Reasons
1. 𝐹𝐴 ≅ 𝑀𝑅 Given
2. 𝐹𝑅 ≅ 𝐹𝑅 Reflexive
3. 𝑚∠1 < 𝑚∠2 Exterior angle Inequality Theorem
4. 𝐹𝑀 > 𝐴𝑅 The Hinge Theorem (SAS Inequality Theorem)

29. EXAMPLE 5
Given:
𝐶𝐸 is a median of LOV
𝑚∠𝐴 > 𝑚∠𝐵
Prove:
𝑚∠𝐿 > 𝑚∠𝑉
Proof:
Statement Reasons
1.
2.
3.
4.
5.
6.

30. EXAMPLE 5
Given:
𝐶𝐸 is a median of LOV
𝑚∠𝐴 > 𝑚∠𝐵
Prove:
𝑚∠𝐿 > 𝑚∠𝑉
Proof:
Statements Reasons
1. 𝐶𝐸 is a median of LOV Given
2. E is the midpoint of 𝐿𝑉 Definition of Median
3. 𝐿𝐸 ≅ 𝐸𝑉 Definition of Midpoint
4. 𝑂𝐸 ≅ 𝑂𝐸 Reflexive
5. 𝑚∠𝐴 > 𝑚∠𝐵 Given
6. 𝑂𝑉 > 𝑂𝐿 SAS Inequality ( Hinge Theorem)