LA CIRCUNFERENCIA

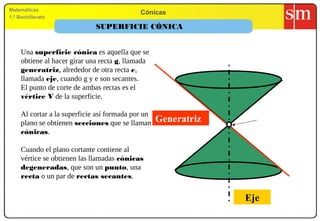
1. Matemáticas
1.º Bachillerato
Cónicas
SUPERFICIE CÓNICA
Una superficie cónica es aquella que se
obtiene al hacer girar una recta g, llamada
generatriz, alrededor de otra recta e,
llamada eje, cuando g y e son secantes.
El punto de corte de ambas rectas es el
vértice V de la superficie.
Al cortar a la superficie así formada por un
plano se obtienen secciones que se llaman
cónicas.
Cuando el plano cortante contiene al
vértice se obtienen las llamadas cónicas
degeneradas, que son un punto, una
recta o un par de rectas secantes.
Generatriz
Eje

2. Matemáticas
1.º Bachillerato
Cónicas
CÓNICAS
DEGENERADAS
Punto Recta Rectas secantes
<α β =α β >α β
α
β
α
β α
β

3. Matemáticas
1.º Bachillerato
Cónicas
Circunferencia:
El plano secante es perpendicular al eje.
Elipse:
El plano secante forma con el eje un ángulo (β) menor
que con las generatrices (α)
En ambos casos la cónica es una curva cerrada y corta a
todas las generatrices
Parábola:
El plano secante es paralelo a una generatriz, cortando a
una sola de las hojas de la superficie cónica. β = α
Hipérbola:
El plano secante forma con el eje un ángulo (β) menor
que con las generatrices (α) y corta a las dos hojas de
la superficie cónica.
En ambos casos la cónica es una curva abierta y no
corta a todas las generatrices.
Circunferencia Elipse
Parábola Hipérbola
CÓNICAS NO DEGENERADAS
β = 90º β > α
β = α β < α

4. Matemáticas
1.º Bachillerato
Cónicas
Circunferencia como sección de un cono
Al cortar la superficie cónica con un plano se obtienen unas curvas que se llaman cónicas.
Las distintas posiciones del plano determinan diferentes cónicas.
Circunferencia: cónica no degenerada que se obtiene cuando el plano secante es
perpendicular al eje del cono, corta a todas las generatrices y no pasa por el vértice.

5. Matemáticas
1.º Bachillerato
Cónicas
C
Estudio sintético de la circunferencia
Circunferencia es el lugar geométrico de los puntos del plano que equidistan de un
punto fijo llamado centro.
Radio
Diámetro
Centro
Cuerda
Arco
C PC

6. Matemáticas
1.º Bachillerato
Cónicas
Ecuación de la
circunferencia
P(x, y) ∈Circunferencia ⇔d(P, C) = r ⇔(x – a)
2
+(y – b)
2
= r
Ecuación analítica de la circunferencia: (x – a)2
+(y – b)2
= r2
x2
+ y2
– 2ax – 2by + a2
+ b2
– r2
= 0
x2
+ y2
+D x + E y + F = 0
Inversamente: dada x2
+ y2
+D x + E y + F = 0 su centro y el radio serán:


–2a = D
–2b = E
a
2
+b
2
–r
2
= F
⇔





a = –
D
2
b = –
E
2
r = a
2
+b
2
–F =
1
2
D
2
+E
2
–4F

7. Matemáticas
1.º Bachillerato
Cónicas
Condiciones para que una ecuación represente a una
circunferencia
kx2
+ky2
–2akx –2bky +k(a2
+b2
–R2
)=0
Ax2
+By2
+Cxy +D x +E y + F = 0
Identificando coeficientes se obtiene:
• De las dos primeras ecuaciones A = B = k.
• Y de las tres últimas: a = –
D
2A ; b = –
E
2A ; R =
1
2A D
2
+E
2
–4AF
• C = 0
Si es negativo no existe circunferencia.

8. Matemáticas
1.º Bachillerato
Cónicas
Posiciones relativas de un punto y una
circunferencia
Si d(P, O) > r el punto P
es exterior
Si d(P, O) = r el punto P
está en la circunferencia
Si d(P, O) < r el punto P
es interior

9. Matemáticas
1.º Bachillerato
Cónicas
Posiciones relativas de una circunferencia y una
recta
• Si d(O, s) > r, la recta s
es exterior.
• Recta y circunferencia
no tienen puntos en
común.
• Si d(O, s) = r, la recta s
es tangente.
• Recta y circunferencia
tienen un punto en
común.
• Si d(O, s) < r, la recta s
es secante.
• Recta y circunferencia
tienen dos puntos en
común.

10. Matemáticas
1.º Bachillerato
Cónicas
Posiciones relativas de una recta y una
circunferencia
Para saber cuántos puntos en común tienen una recta a x + b y + c=0 y una circunferencia
Ax2
+ Ay2
+ Bx + Cy + D = 0 hemos de saber cuántas soluciones tiene el sistema
a x + b y + c = 0
Ax2
+ Ay2
+ Bx + Cy + D = 0
Mx2
+ Nx + P = 0
Al despejar y de la ecuación de arriba y sustituir en la de abajo obtenemos
∆ = N2
- 4 M P > 0 ⇔
⇔ dos soluciones ⇔
⇔ dos puntos de contacto
Recta secante
∆ = N2
- 4 M P = 0 ⇔
⇔ una solución ⇔
⇔ un punto de contacto
Recta tangente
∆ = N2
- 4 M P < 0 ⇔
⇔ sin solución ⇔
⇔ sin puntos de contacto
Recta exterior
•
• •

11. Matemáticas
1.º Bachillerato
Cónicas
Posiciones relativas de dos
circunferencias
• Si d(O, O') > r + r', las
circunferencias son
exteriores.
• Las circunferencias no
tienen puntos en común.
• Si d(O, O') = r + r', las
circunferencias son
tangentes exteriores.
• Si d(O, O') = r – r', las
circunferencias son
tangentes interiores.
• Las circunferencias
tienen un punto en
común.
• Si d(O, O') < r – r', las
circunferencias son
interiores.
• Si además tienen el
mismo centro son
concéntricas.
• Las circunferencias no
tienen puntos en común.

12. Matemáticas
1.º Bachillerato
Cónicas
Potencia de un punto respecto a una
circunferencia
• Los triángulos PAB' y PA'B son semejantes ⇒ PA . PB = PA' . PB‘
• Se define Potc(P) = PA . PB = PA' . PB'

13. Matemáticas
1.º Bachillerato
Cónicas
Expresión analítica de la
potencia
Potc(P) = PA . PB = (d – r) (d + r) = d2
– r2
= (xo – a)2
+ (yo – b)2
– r2
d = (xo–a)
2
+(yo–b)
2
Por tanto: para hallar la potencia de un punto respecto a una circunferencia
se sustituyen las coordenadas del punto en la ecuación de la circunferencia.

14. Matemáticas
1.º Bachillerato
Cónicas
Potencia y posición
relativa
P exterior a la
circunferencia ⇔
Potc(P) > 0
P interior a la
circunferencia ⇔
Potc(P) < 0
P sobre la
circunferencia ⇔
Potc(P) = 0

15. Matemáticas
1.º Bachillerato
Cónicas
• Sean C1: x2
+ y2
+ Dx + Ey + F = 0 y C2 : x2
+ y2
+ D'x + E'y + F' = 0.
• Para que un punto P(x, y) pertenezca al eje radical se ha de cumplir que PotC
1
(P) =
= PotC
2
(P) . Es decir:
x2
+ y2
+ Dx + Ey + F = x2
+ y2
+ D'x + E'y + F' ⇔
⇔ (D – D') x + (E – E') y + (F – F') = 0
Eje radical de dos
circunferencias
Se define el eje radical de dos circunferencias como el lugar geométrico de los
puntos del planos que tienen igual potencia respecto de ambas.
Por tanto: el eje radical de dos circunferencias es una recta.

16. Matemáticas
1.º Bachillerato
Cónicas
Estudio geométrico del eje radical de dos
circunferencias
El eje radical es siempre perpendicular a la línea de centros.

17. Matemáticas
1.º Bachillerato
Cónicas
Parábola como secciones de un cono
Parábola: cónica no degenerada que se obtiene cuando el plano secante es
oblicuo al eje del cono, paralelo a una generatriz y no pasa por el vértice.

18. Matemáticas
1.º Bachillerato
Cónicas
P(x, y) ∈parábola ⇔d(P, F) = d(P, d) ⇔x
2
+






y –
p
2
2
=







y +
p
2
0
2
+ 1
2
Ecuación de la parábola: eje en OY y ramas hacia
arriba
Para obtener una ecuación sencilla de la parábola, se puede situar el foco, F, en el eje de
ordenadas simétrico respecto al origen de coordenadas de la directriz, d, que se sitúa
paralela al eje de abscisas. La distancia desde el foco a la directriz se llama parámetro.
Podemos entonces tomar (por ejemplo): F(0, p/2) y d: y = – p/2
Eliminando radicales: x2
= 2py
• P(x, y)

19. Matemáticas
1.º Bachillerato
Cónicas
Estudio sintético de la
parábola
La parábola es el lugar geométrico de los puntos del plano, P, que equidistan de un
punto fijo F llamado foco y de una recta d llamada directriz.
• P
Radio vector
V: vértice
Eje
Cuerda focal
d(P, F)
d(P, d)
e = = 1
La excentricidad de la
parábola es 1.• F: foco
d: directriz
Parámetro

20. Matemáticas
1.º Bachillerato
Cónicas
Ecuación de la parábola: eje en OY y ramas hacia
abajo
Para obtener una ecuación sencilla de la parábola se puede situar el foco, F, en el eje de
ordenadas simétrico respecto al origen de coordenadas de la directriz, d, que se sitúa
paralela al eje de abscisas. La distancia desde el foco a la directriz se llama parámetro.
Podemos entonces tomar (por ejemplo): F(0, – p/2) y d: y = p/2
P(x, y) ∈parábola ⇔d(P, F) = d(P, d) ⇔x
2
+






y +
p
2
2
=







y –
p
2
0
2
+ 1
2
Eliminando radicales: x2
= – 2py
• P(x, y)

21. Matemáticas
1.º Bachillerato
Cónicas
Ecuación de la parábola: eje en OX y ramas hacia la
derecha
Para obtener una ecuación sencilla de la parábola se puede situar el foco, F, en el eje de
abcisas simétrico respecto al origen de coordenadas de la directriz, d, que se sitúa
paralela al eje de abscisas. La distancia desde el foco a la directriz se llama parámetro.
Podemos entonces tomar (por ejemplo): F(p/2, 0) y d: x = – p/2
P(x, y) ∈parábola ⇔d(P, F) = d(P, d) ⇔






x –
p
2
2
+ y
2
=







x +
p
2
1
2
+ 0
2
Eliminando radicales: y2
= 2px
• P(x, y)

22. Matemáticas
1.º Bachillerato
Cónicas
Ecuación de la parábola: eje en OX y ramas hacia la
izquierda
Para obtener una ecuación sencilla de la parábola se puede situar el foco, F, en el eje
de abcisas simétrico respecto al origen de coordenadas de la directriz, d, que se sitúa
paralela al eje de abscisas. La distancia desde el foco a la directriz se llama parámetro.
Podemos entonces tomar (por ejemplo): F(– p/2, 0) y d: x = p/2
P(x, y) ∈parábola ⇔d(P, F) = d(P, d) ⇔






x +
p
2
2
+ y
2
=







x –
p
2
1
2
+ 0
2
Eliminando radicales: y2
= – 2px
•
P(x, y)

23. Matemáticas
1.º Bachillerato
Cónicas
Tangente y normal a una parábola en un
punto
• Ecuación de la recta tangente: y – f(xo) = f '(xo) (x – xo)
• Ecuación de la recta normal: y – f(xo) = (–1/ f '(xo)) (x – xo)
Propiedad de la tangente:
La tangente y la normal son las bisectrices de los ángulos que forman el radio vector de un punto P y
una recta paralela al eje que pasa por P.
Propiedad del foco:
• Todo rayo que sale del foco se refleja en la parábola con dirección paralela al eje.
• Todo rayo que llega paralelo al eje de la parábola se refleja sobre el foco.

24. Matemáticas
1.º Bachillerato
Cónicas
Elipse como secciones de un cono
Elipse: cónica no degenerada que se obtiene cuando el plano secante es oblicuo al
eje del cono, corta a todas las generatrices y no pasa por el vértice.

25. Matemáticas
1.º Bachillerato
Cónicas
Estudio sintético de la
elipse
La elipse es el lugar geométrico de los puntos del plano, P, cuya suma de distancias
a dos puntos fijos, llamados focos (F y F'), es constante, 2a. Por tanto: PF + PF' = 2a
Eje mayor
Eje
menor
Vértices
Radio vector
Radiovector
Eje focal
Eje secundario

26. Matemáticas
1.º Bachillerato
Cónicas
• BF + BF' = 2a ⇒ (BF = BF') ⇒ 2 BF = 2a ⇒ BF = a
Segmentos de la elipse. Relación
fundamental
• A'A = A'F + FA = A'F + A'F' = 2a ⇒ OA = OA' = a
aa
• BB' = 2b ⇒ OB = OB' = b
• FF' = 2c ⇒ OF = OF' = c
a
c
b
a2
= b2
+ c2

27. Matemáticas
1.º Bachillerato
Cónicas
• e = c/a
• 0 < e < 1 ya que 0 < c < a
• En la medida en que e se aproxima a 0 la elipse se parece más a una circunferencia.
• En la medida en que e se aproxima a 1 la elipse se parece más a un segmento.
Excentricidad de la
elipse
e = 0.1
e = 0.3
e = 0.5
e = 0.7
e = 0.9
Sucesivas elipses en las
que a = 5.
Los focos, cuando e pasa de
1 a 0, van acercándose
cada vez más al centro.

28. Matemáticas
1.º Bachillerato
Cónicas
Ecuación de la
elipse
Para obtener una ecuación sencilla de la elipse se sitúan los focos en el eje de abscisas
simétricos respecto al origen de coordenadas, por lo que el centro de la elipse quedará
en (0,0). Las coordenadas de los focos serán entonces F(c, 0) y F'(–c, 0).
P(x, y) ∈elipse ⇔PF + PF' = 2a ⇔(x – c)
2
+y
2
+ (x + c)
2
+y
2
= 2a
• Eliminando radicales: (a2
– c2
) x2
+ a2
y2
= a2
(a2
– c2
).
• Como a2
– c2
= b2
. Obtenemos: b2
x2
+ a2
y2
= a2
b2
, y dividiendo por a2
b2
:
x
2
a
2 +
y
2
b
2 = 1

29. Matemáticas
1.º Bachillerato
Cónicas
Traslación de
vector guía
→
v = (1,4)
Ecuación general de las
cónicas
• Las ecuaciones más sencillas de las cónicas se obtienen cuando los ejes
coordenados coinciden con sus ejes.
• ¿Qué forma tienen dichas ecuaciones cuando la cónica está situada en cualquier
parte del plano?
Elipse de ecuación
x2
9 +
y2
4 = 1
Elipse de ecuación
(x−1)2
9 +
(y−4)2
4 = 1
Giro de centro
el origen y
amplitud 45º
La ecuación general de una
cónica es
Ax2
+Bxy+Cy2
+Dx+Ey+F=0
donde A, B y C no son nulos
a la vez.
Elipse de ecuación
(
1
2
(x+y) − 1 )2
9 +
(
1
2
(−x+y) − 4)2
4 = 1

30. Matemáticas
1.º Bachillerato
Cónicas
Tangente y normal a una elipse en un
punto
• Ecuación de la recta tangente: y – f(xo) = f '(xo) (x – xo)
• Ecuación de la recta normal: y – f(xo) = (–1/ f '(xo)) (x – xo)
Propiedad de la tangente: los radio-vectores del punto P forman el mismo
ángulo con la recta tangente en dicho punto.

31. Matemáticas
1.º Bachillerato
Cónicas
Hipérbola como secciones de un
cono
Hipérbola: cónica no degenerada que se obtiene cuando el plano es paralelo al eje
del cono y no pasa por el vértice.

32. Matemáticas
1.º Bachillerato
Cónicas
Estudio sintético de la
hipérbola
La hipérbola es el lugar geométrico de los puntos del plano, P, cuya diferencia de distancias, en
valor absoluto, a dos puntos fijos, llamados focos (F y F'), es constante, 2a.
Por tanto: |PF – PF'| = 2a
Eje focal
Eje secundario
Centro
Vértices
Radio vector
Radiovector
Eje mayor
Eje
menor

33. Matemáticas
1.º Bachillerato
Cónicas
Asíntotas de la hipérbola. Relación
fundamental
Asíntota: y = (b/a) x
Asíntota: y = – (b/a) x
2a
2ba
b c c2
= a2
+ b2
• A'A = AF' – A'F' = AF' – AF = 2a ⇒ OA = OA' = a
• BB' = 2b ⇒ OB = OB' = b
• FF' = 2c ⇒ OF = OF' = c
•
F
•
F'

34. Matemáticas
1.º Bachillerato
Cónicas
Excentricidad de la
hipérbola
• e = c/a
• e > 1 ya que c > a
• En la medida en que e se hace muy grande las ramas de la hipérbola se abren cada vez más.
• En la medida en que e se aproxima a 1 las ramas se cierran sobre el eje OX.
Sucesivas hipérbolas en las que a = 5.
Los focos, al crecer e, se van alejando del
centro.
e = 3
e = 1.1
e = 2

35. Matemáticas
1.º Bachillerato
Cónicas
Ecuación de la
hipérbola
Para obtener una ecuación sencilla de la hipérbola se sitúan los focos en el eje de abscisas
simétricos respecto al origen de coordenadas, por lo que el centro de la elipse quedará en (0,0).
Las coordenadas de los focos serán entonces F(c, 0) y F'(–c, 0).
P(x, y) ∈hipérbola ⇔|PF – PF'| = 2a ⇔|(x-c)
2
+y
2
– (x+c)
2
+y
2
|= 2a
• Eliminando radicales: (c2
– a2
) x2
– a2
y2
= a2
(c2
– a2
).
• Como a2
+ b2
= c2
. Obtenemos: b2
x2
– a2
y2
= a2
b2
, y dividiendo por a2
b2
:
x
2
a
2 –
y
2
b
2 = 1

36. Matemáticas
1.º Bachillerato
Cónicas
Tangente y normal a una hipérbola en un
punto
• Ecuación de la recta tangente: y – f(xo) = f '(xo) (x – xo)
• Ecuación de la recta normal: y – f(xo) = (–1/ f '(xo)) (x – xo)
Propiedad de la tangente: los radio-vectores del punto P forman el mismo ángulo con la recta
tangente en dicho punto.

37. Matemáticas
1.º Bachillerato
Cónicas
Clasificación de las
cónicas
La gráfica de cualquier cónica no degenerada de ecuación
Ax2
+ Bxy + Cy2
+ Dx + Ey + F = 0
• es una elipse si: B2
– 4AC < 0
• es una parábola si: B2
– 4AC = 0
• es una hipérbola si: B2
– 4AC > 0
Además si B = 0 los ejes de la cónica son paralelos a los ejes coordenados, y si B ≠ 0
la cónica tiene los ejes girados respecto a los ejes cartesianos.
La ecuación general de esta
cónica es
Ax2
+Bxy+Cy2
+Dx+Ey+F=0
con B = 0 y B2
– 4AC < 0
La ecuación general de esta
cónica es
Ax2
+Bxy+Cy2
+Dx+Ey+F=0
con B = 0 y B2
– 4AC > 0
La ecuación general de esta
cónica es
Ax2
+Bxy+Cy2
+Dx+Ey+F=0
con B = 0 y B2
– 4AC = 0

38. Matemáticas
1.º Bachillerato
Cónicas
Otra clasificación de las
cónicas
Dado un punto F llamado foco, una
recta fija d (que no pase por F) llamada
directriz y un número e > 0, el conjunto
de los puntos P del plano tal que
d(P, F) = e . d(P, d)
es una cónica de excentricidad e.
• Si e < 1 es una elipse
• Si e = 1 es una parábola
• Si e > 1 es una hipérbola
Elipses
Parábola
Hipérbola