Movimiento de la partícula

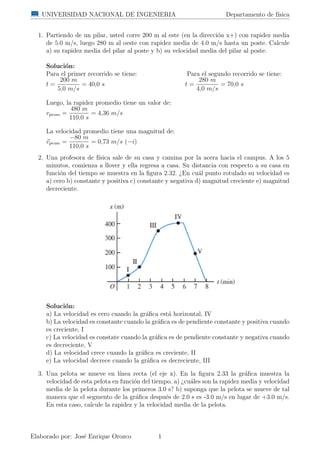
1. UNIVERSIDAD NACIONAL DE INGENIERIA Departamento de f´ısica
1. Partiendo de un pilar, usted corre 200 m al este (en la direcci´on x+) con rapidez media
de 5.0 m/s, luego 280 m al oeste con rapidez media de 4.0 m/s hasta un poste. Calcule
a) su rapidez media del pilar al poste y b) su velocidad media del pilar al poste.
Soluci´on:
Para el primer recorrido se tiene: Para el segundo recorrido se tiene:
t =
200 m
5,0 m/s
= 40,0 s t =
280 m
4,0 m/s
= 70,0 s
Luego, la rapidez promedio tiene un valor de:
vprom =
480 m
110,0 s
= 4,36 m/s
La velocidad promedio tiene una magnitud de:
vprom =
−80 m
110,0 s
= 0,73 m/s (−i)
2. Una profesora de f´ısica sale de su casa y camina por la acera hacia el campus. A los 5
minutos, comienza a llover y ella regresa a casa. Su distancia con respecto a su casa en
funci´on del tiempo se muestra en la figura 2.32. ¿En cu´al punto rotulado su velocidad es
a) cero b) constante y positiva c) constante y negativa d) magnitud creciente e) magnitud
decreciente.
Soluci´on:
a) La velocidad es cero cuando la gr´afica est´a horizontal, IV
b) La velocidad es constante cuando la gr´afica es de pendiente constante y positiva cuando
es creciente, I
c) La velocidad es constate cuando la gr´afica es de pendiente constante y negativa cuando
es decreciente, V
d) La velocidad crece cuando la gr´afica es creciente, II
e) La velocidad decrece cuando la gr´afica es decreciente, III
3. Una pelota se mueve en l´ınea recta (el eje x). En la figura 2.33 la gr´afica muestra la
velocidad de esta pelota en funci´on del tiempo. a) ¿cu´ales son la rapidez media y velocidad
media de la pelota durante los primeros 3.0 s? b) suponga que la pelota se mueve de tal
manera que el segmento de la gr´afica despu´es de 2.0 s es -3.0 m/s en lugar de +3.0 m/s.
En esta caso, calcule la rapidez y la velocidad media de la pelota.
Elaborado por: Jos´e Enrique Orozco 1

2. UNIVERSIDAD NACIONAL DE INGENIERIA Departamento de f´ısica
Soluci´on:
a) De t = 0 a t = 2,0 s v = 2,0 m/s ∆x = (2,0 m/s)(2,0 s) = 4,0 m
Para t=2.0 s a t=3.0 s, v=3.0 m/s. ∆x = (3,0 m/s)(1,0 s) = 3,0 m.
La distancia total recorrida es, ∆x = 7,0 m, la rapidez promedio es:
vprom =
7,0 m
3,0 s
= 2,33 m/s
b) Para t=2.0 s a t=3.0 s, v=-3.0 m/s. ∆x = (−3,0 m/s)(1,0 s) = −3,0 m.
El desplazamiento ser´ıa: ∆x = 4,0 m + (−3,0 m) = +1,0 m
v =
1,0 m
3,0 s
= 0,33 m/s
4. La figura muestra la velocidad de un autom´ovil solar en funci´on del tiempo. El conductor
acelera desde un letrero de alto, viaja 20 s con rapidez constante de 60 km/h y frena
para detenerse 40 s despu´es de partir del letrero. Calcule la aceleraci´on media para estos
intervalos: i) de t=0 a t=5 s ii) t=30 s a t=40 s iii) t=10 a t=30 s iv) t=0 a t=40 s. ¿Cu´al
es la aceleraci´on instant´anea en t=20 s y en t=35 s?
Elaborado por: Jos´e Enrique Orozco 2

3. UNIVERSIDAD NACIONAL DE INGENIERIA Departamento de f´ısica
Soluci´on:
60 km/h = 16,7 m/s
a)
i) aprom =
16,7 m/s − 0
10 s
= 1,67 m/s2
ii) aprom =
0 − 16,7 m/s
10 s
= −1,67 m/s
iii) ∆v = 0 → a = 0
iv) ∆v = 0 → a = 0
b) En t=20 s ∆v = 0 por tanto a=0. Para t=35 s a = −167 m/s2
5. El cuerpo humano puede sobrevivir a un trauma por aceleraci´on, si la magnitud de la
aceleraci´on es menor que 250 m/s2
. Si usted sufre un accidente automovil´ıstico con rapidez
inicial de 105 km/h y es detenido por una bolsa de aire que se infla desde el tablero, ¿en
qu´e distancia debe ser detenido por la bolsa de aire para sobrevivir al percance?
Soluci´on:
a = −250 m/s2
, 105 km/h = 29,17 m/s.
v0 = 29,17 m/s, v = 0.
v2
= v0
2
+ 2a∆x → ∆x =
0 − (29,17 m/s)2
2(−250 m/s2)
= 1,70 m
6. Un gato camina el l´ınea recta en lo que llamaremos eje x con la direcci´on positiva a la
derecha. Usted, que es un f´ısico observador. Efect´ua mediciones del movimiento del gato y
elabora un gr´afico de la velocidad del felino en funci´on del tiempo. Determine la velocidad
del gato en t=4 s y en t=7 s. b) ¿qu´e aceleraci´on tiene el gato en t=3 s? ¿en t=6 s? ¿en
t=7 s? c) ¿qu´e distancia cubre el gato durante los primeros 4.5 s? ¿entre t=0 y t=7.5 s?
Soluci´on:
a) para t=4 s, v=2.7 cm/s. En t=7 s, v=1.3 cm/s
b) a = −
8 cm/s
6 s
= −1,3 cm/s2
. Debido a que la gr´afica es de pendiente constante, la
aceleraci´on es la misma para todos los instantes de tiempos.
c) ∆x = v0t + 1
2
at2
. Para t=4.5
∆x = (8 cm/s)(4,5 s) + 1
2
(−1,3 cm/s2
)(4,5 s)2
= 22,8 cm. Para t=7.5 s
∆x = (8 cm/s)(7,5 s) + 1
2
(−1,3 cm/s2
)(7,5 s)2
= 23,4 cm
Elaborado por: Jos´e Enrique Orozco 3

4. UNIVERSIDAD NACIONAL DE INGENIERIA Departamento de f´ısica
7. Si una pulga puede saltar 0.440 m hacia arriba, ¿qu´e rapidez inicial tiene al separarse del
suelo? ¿cu´anto tiempo est´a en el aire?
Soluci´on:
a) v2
= v0
2
+ 2a∆x → v0 =
√
v2 − 2a∆x, considerando que a=-9.8 m/s2
v0 = 0 − 2(−9,8 m/s2)(0,440 m)
v0 = 2,94 m/s
b) v = v0 + a · t → t =
v − v0
a
t =
0 − 2,94 m/s
−9,8 m/s2
t = 0,3 s → tiempo que tarde en subir, el tiempo en el aire es dos veces el tiempo de
subida, por tanto, el tiempo que tarda en el aire es t = 0,6 s
8. Un cohete de 7500 kg despega verticalmente desde la plataforma de lanzamiento con una
aceleraci´on constante hacia arriba de 2.25 s/s2
y no sufre resistencia del aire considerable.
Cuando alcanza su altura de 525 m, sus motores fallan repentinamente y ahora la ´unica
fuerza que act´ua sobre ´el es la gravedad. a) ¿Cu´al es la atura m´axima que alcanzar´a este
cohete desde la plataforma de lanzamiento? b) despu´es de que el motor falla, ¿cu´anto
tiempo pasar´a antes de que se estrelle con la plataforma de lanzamiento, y qu´e rapidez
tendr´a justo antes del impacto? c) dibuje las gr´aficas ay − t, vy − t y y − t del movimiento
del cohete desde el instante en que despega hasta el instante justo antes de chocar contra
la plataforma de lanzamiento.
Soluci´on:
v2
= v0
2
+ 2a∆y → v 2(2,25 m/s2)(525 m)
v = 48,6 m/s
∆y =
v2
− v0
2
2a
∆y =
0 − (48,6 m/s)2
2(−9,8 m/s2)
∆y = 121 m, considerando que y0 = 525, se tiene que la altura m´axima es y = 121 m +
525 m = 646 m
v2
= v0
2
+ 2a∆y → v = − (48,6 m/s)2 + 2(−9,8 m/s2)(−525 m)
v = −112 m/s
t =
v − v0
a
→ t =
−112 m/s − 48,6 m/s
−9,8 m/s2
t = 16,4 s c) Considerando todos los valores dados y calculados, podemos utilizar el
m´etodo de marcaci´on de puntos y esbozar la interpretaci´on geom´etrica de nuestros datos.
Elaborado por: Jos´e Enrique Orozco 4

5. UNIVERSIDAD NACIONAL DE INGENIERIA Departamento de f´ısica
9. El tripulante de un globo aerost´atico que sube verticalmente con velocidad constante de
5 m/s, suelta un saco de arena cuando el globo est´a a 40 m sobre el suelo (vea la figura).
Despu´es de que se suelta, el saco est´a en ca´ıda libre. a) Calcule la posici´on y velocidad del
saco a 0.250 s y 1 s despu´es de soltarse. b) ¿Cu´antos segundos tardar´a el saco en chocar
con el suelo despu´es de soltarse? c) ¿Con qu´e rapidez chocar´a? d) ¿Qu´e altura m´axima
alcanza el saco sobre el suelo? e) Dibuje las gr´aicas ay − t, vy − t y y − t
Soluci´on:
a) para t=0.250 s
∆y = v0t + 1
2
at2
→ ∆y = (5 m/s)(0,250 s) + 1
2
(−9,8 m/s3
)(0,250)2
∆y = 0,94 m
v = v0 + at → v = 5 m/s + (−9,8 m/s2
)(0,250 s) = 2,55 m/s
para t=1 s
∆y = (5 m/s)(1 s) + 1
2
(−9,8 m/s2
)(1 s)
∆y = 0,10 m
v = 5 m/s + (−9,8 m/s2
)(1 s)
v = −4,80 m/s
b) −40 m = (5 m/s)t + 1
2
(−9,8 m/s2
)t2
, utilizando la ecuaci´on cuadr´atica, tenemos:
t =
5 ± 25 − 4(4,9)(−40)
2(4,9)
t = (0,51 ± 2,90) s, el ´unico valor f´ısicamente posible es t = 0,21 + 2,90 = 3,41 s
c) v = 5 m/s + (−9,8 m/s2
)(3,41 s) = −28,4 m/s
d) ∆y =
0 − (5 m/s)2
2(−9,8 m/s2)
= 1,28 m
e)
Elaborado por: Jos´e Enrique Orozco 5

6. UNIVERSIDAD NACIONAL DE INGENIERIA Departamento de f´ısica
10. Un libro de f´ısica se desliza sobre una mesa horizontal a 1.10 m/s cae al piso en 0.350 s.
Ignore la resistencia del aire. Calcule a) la altura de la mesa b) la distancia horizontal del
borde de la mesa al punto donde cae el libre c) las componentes horizontal y vertical, y
la magnitud y direcci´on, de la velocidad del libro justo antes de tocar el piso. d) Dibuje
las gr´aficas x − t, y − t, vx − t, vy − t
Soluci´on:
∆y = v0yt + 1
2
at2
→ ∆y = 0 + 1
2
(−9,8 m/s2
)(0,350 s)2
∆y = −0,6 m. La mesa tiene 60 cm de altura.
b) ∆x = v0xt
∆x = (1,10 m/s)(0,350 s)
∆x = 0,358 m
vx = v0x = 1,10 m/s
vy = v0y + at → vy = 0 + (−9,8 m/s2
)(0,350 s) = −3,43 m/s
v = vy
2 + vx
2 → v = (−3,43 m/s)2 + (1,10 m/s)2
v = 3,60 m/s
tanα =
vy
vx
=
−3,43
1,10
α = −72,2o
(sentido horario)
c)
11. Un autom´ovil llega a un puente durante una tormenta y el conductor descubre que las
aguas se lo han llevado. El conductor debe llegar al otro lado, as´ı que decide intentar
saltar la brecha con su auto. La orilla en la que se encuentra est´a a 21.3 m arriba del
r´ıo, mientras que la orilla opuesta est´a a s´olo 1.8 m sobre las aguas. El r´ıo es un torrente
Elaborado por: Jos´e Enrique Orozco 6

7. UNIVERSIDAD NACIONAL DE INGENIERIA Departamento de f´ısica
embravecido con una anchura de 61 m. a) ¿Qu´e tan r´apido deber´a ir el auto cuando llegue
a la orilla para librar el r´ıo y llegar a salvo al otro lado? b) ¿Qu´e rapidez tendr´a el auto
justo antes de que aterrice en la orilla opuesta?
Soluci´on:
∆y = v0yt + 1
2
at2
→ t =
2(19,5 m)
9,80 m/s2
= 1,99 s
∆x = v0xt → v0x =
61 m
1,99 s
= 30,6 m/s
b) v = vy
2 + vx
2 → v = (30,6 m/s)2 + (−19,6 m/s)2 = 36,33 m/s
12. Se dispara una proyectil desde el nivel del suelo con una velocidad inicial de 80 m/s
a 60o
por encima de la horizontal sin que sufra resistencia del aire. a) Determine las
componentes horizontal y vertical de la velocidad inicial del proyectil. b) ¿Cu´anto tarda
el proyectil en alcanzar su punto m´as alto? c) Calcule su altura m´axima por encima del
suelo. d) ¿Qu´e tan lejos del punto de lanzamiento cae el proyectil al suelo? e) Determine
las componentes horizontal y vertical de su aceleraci´on y velocidad en el punto de su
altura m´axima.
Soluci´on:
a) v0x = v0cosθ → v0x = (80 m/s)cos60o
v0x = 40 m/s
v0y = v0senθ → v0y = (80 m/s)sen60o
v0y = 69,3 m/s
b) vy = v0y + at → t =
0 − 69,3 m/s
−9,8 m/s
= 7,07 s
c) v2
y = v0y
2
+ 2a∆y → ∆y =
0 − (69,3 m/s)2
2(−9,8 m/s2)
= 245 m
d) ∆x = vxt → ∆x = (40 m/s)(14,14 s) = 566 m
e) Al alcanzar su altura m´axima las componentes de su velocidad son vx = 40 m/s y
vy = 0. En todo punto ax = 0 y ay = −9,8 m/s2
13. Un pelotero de grandes ligas batea una pelota de de modo que sale del bate con una
rapidez de 30 m/s y un ´angulo de 36.9o
sobre la horizontal. Ignore la resistencia del aire.
a) ¿En cu´ales dos instantes la pelota estuvo a 10 m sobre el punto en que sali´o del bate?
b) Obtenga las componentes horizontal y vertical de la velocidad de la pelota en cada uno
de los instantes calculados en el inciso a). c) ¿Qu´e magnitud y direcci´on ten´ıa la velocidad
de la pelota al regresar al nivel en el que se bate´o?
Soluci´on:
v0x = v0cosθ → v0x = (30 m/s)cos36,9o
v0x = 24 m/s
v0y = v0senθ → v0y = (30 m/s)sen36,9o
v0y = 18 m/s
∆y = v0yt + 1
2
at2
→ 10 m = (18 m/s)t + 1
2
(−9,8 m/s2
)t2
Elaborado por: Jos´e Enrique Orozco 7

8. UNIVERSIDAD NACIONAL DE INGENIERIA Departamento de f´ısica
t =
18 ± 324 − 4(4,9)(10)
2(4,9)
t = (1,837 ± 1,154)s → t1 = 0,683 s y t2 = 2,99 s
para t1 = 0,683 s vy = 18 m/s + (−9,8 m/s)(0,683) = 11,3 m/s
para t2 = 2,99 s vy = 18 m/s + (−9,8 m/s)(2,99) = −11,3 m/s
vx = v0x = 24 m/s
Elaborado por: Jos´e Enrique Orozco 8