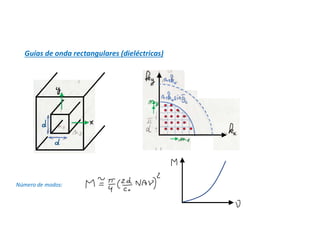
Guías de onda rectangulares (dieléctricas)
Número de modos:

Guías circulares (fibras)
Fibra = guía de onda cilíndrica (sílice SiO2)
Multimode (MM) Single mode (SM)
Indice escalonado
(Step index, SI)
Indice graduado
(Graded index, GI) Diámetros: 8/125
Diámetros: 60, 62.5, 85/125

Rayos meridionales:
Rayos oblicuos (“skewed”):
Trayectoria helicoidal (polígono)
En un plano meridional

Ec. de Helmholtz:
(coordenadas cartesianas)
En coordenadas
cilíndricas:
Separación de variables:
U(x,y,z)
Núcleo:
(n = n1)
Revestimiento:
(n = n2)
l = número de modo acimutal
Ecuaciones
de Bessel
kt

j

P(r,,z)
Er
E
Ez

O z
d2/dx2 + d2/dy2 + d2/dz2
Onda viajera en z
Periódica en , periodo 2/l

Funciones de Bessel ordinarias de 1er tipo, orden l
Funciones de Bessel modificadas de 1er tipo, orden l
2º tipo
2º tipo
Jl: Kl:
Campo eléctrico E
Intensidad I  E2
Dependencia radial de los campos:
Nl: Il:
l = 0
m = 1
l = 0
m = 3
l = 3
m = 3
l = 3
m = 1

z z
Periodo acimutal = 2r/l  r
Dependencia acimutal de los campos:
=> k =  en r = 0; sin embargo, no hay singularidad
ya que en el centro el campo = 0 (para l  0)
k = l/r r-1 : vector de onda que
depende de la posición!
Ejemplo para l = 8

Frecuencia normalizada
= frecuencia normalizada

Ecuación de eigenvalores
A, B, C, D calculadas gracias a condiciones de frontera:
1 ecuación para cada valor de l = 0, 1, 2 …
: 1 sola solución, la solución trivial A = B = C = D = 0
Modos guiados existen solo si:

l
m
0
1
lmax
=> No existen modos guiados en ese caso
Ecuación de eigenvalores

v
v
HE11
HE21
TE01
TM01
HE12
HE31
EH11
b
n1
n2

k1
k2

HElm : Ez 
HE-lm : Ez 
HElm + HE-lm : Ez 
HElm - HE-lm : Ez 
Modos
degenerados
Modos
degenerados
z
z
z
z

Ejemplo: HE11 (fundamental):
Ez  ó
Er  Ez 
E  dEz /d  -
E
Er
Er
E

r
r

 = 0
 = /4
 = /2
Er
E
 = 
E
H
2 modos
fundamentales
HE11 degenerados
ortogonales
También existen
componentes Ez, Hz
!

0 = 1
Caso l = 0 (meridionales): TM01 y TE01
E
Er
Er
E
 = 0
 = /4
 = /2
Er
E
 = 
Ez  ó
Er  Ez  1
E  dEz /d  - = 0 0 = 1
= 0
0
E
Er
Er
E
 = 0
 = /4
 = /2
Er
E
 = 
E
H
= TM01
= TE01
z z

Ejemplo: HE21
Ez  ó
Er  Ez 
E  dEz /d  -
E
H
E
Er
Er
E
 = 0
 = /4
 = /2
Er
E
 = 
E
H
E
Er
Er
E
 = 0
 = /4
 = /2
Er
E
 = 
2 modos HE21
degenerados
ortogonales

Weakly guiding approximation (guiado débil): n1  n2,  << 1
Componentes longitudinales Ez y Hz  0: modos TEM
Ec. de eigenvalores:
n1  n2

Caso
Misma ec. con
diferencia de 2 en l
Soluciones EHlm
= soluciones HEl+2,m

HE11
HE21
TE01
TM01
HE12
HE31
EH11
b
n1
n2

k1
k2
Modos degenerados: HE11 LP01
HE21, TE01, TM01 LP11
EH11, HE31 LP21
HE12 LP02

Ejemplo: L = 0 (l = 1)
0 2
J0
J1 J2
0
1
u = 0
v = V
u = V
v = 0

+ +
+
TODOS los modos LP son linealmente polarizados
LP01 (HE11):
2 modos
ortogonales
degenerados
? =
LP11 (HE21, TE01, TM01):
=
- =
TM01
HE21
=
- =
TE01
HE21
4 modos ortogonales degenerados
I = 0
Regiones
intensas

Etc.
+
? = +
? =
LP21 : LP31 :
4 modos ortogonales degenerados para cada l  0, m (2 modos si l = 0)
En coordenadas
cartesianas, 1 sola
componente E (x o y)  0 !!
+ 1 de H (y o x)
2 componentes  0

LP01:
LP02:

sin2
2
0 
LP34:
Corte r = Cste
Corte  = Cste
I
a
0 r
I
J3
2
K3
2
E I
Interfaz
I = 0

Exacto Guiado débil
Nomenclatura: HE, EH, TE, TM Todos los modos son LP
HE, EH (~90% de los modos en MMF):
6 componentes E y H  0
TE, TM: 3 (Ez o Hz  0)
Todos los modos son TEM: Ez y Hz = 0
Solo 2 componentes  0: Ex(y) y Hy(x)
para TODOS los modos
b
V
b
V
La aproximación del guiado débil es un formalismo mucho más simple en
diversos aspectos:
Menos curvas (pero
número total de
modos se conserva:
mayor número de
modos degenerados
entre sí)

b
n1
n2

k1
k2 V
LP01
LP11
LP21
LP02
Frecuencias de corte
Vc01 Vc11
Vc21 = Vc02
Frecuencias de corte de LPLm = m-ésima raíz de JL-1(u)/JL(u)
Caso u = 0:
JL-1(0) = 0
pero JL-1(0)/JL(0)  0
para L  2
! VC(LPLm) = VC Lm = m-ésima raíz de JL-1(u)
(descartando la raíz u = 0 si L  2)
LP01 : 1a raíz de J-1(u) = -J1(u): 0
LP11 : 1a raíz de J0(u) = 2.405
LP02 : 2a raíz de J-1(u) = -J1(u): ~3.8
LP21 : 1a raíz de J1(u): 0 3.8
Ejemplos:
0 2
J0
J1 J2
0
1
2.405
(descartando 0)

Longitud de onda de corte (LP11)
Monomodal si V < Vc
0 > c
SMF-28:
c (LP11) = 1260 nm
Ejemplo:
b
LP01
LP11
LP21
LP02
Vc01 Vc11
Monomodal
(SM)
Multimodal
(MM)
V
c11

Monomodal
(SM)
Multimodal
(MM)
Vc (LP11) = 2.405
Monomodal a 1550 nm,
Multimodal a 750 nm

 4 (modos degenerados)
V - (l-0.5)/2

V
(l-0.5)/2
0
V 10
5
0
10
20
30
40
50
M
Número M de modos
4
2
radial
acimutal
ambos

Taylor (x <<):
Índice “generalizado”
q = (l + 2m)2
 c2 = c0/n2 !
q
M
0
vg
c1
(1 - )c1
4
2
Velocidad de grupo:
vg
v
Taylor (x <<):
kt

Orden alto:
Orden bajo: