Ejercicios vibacion de red cristalina

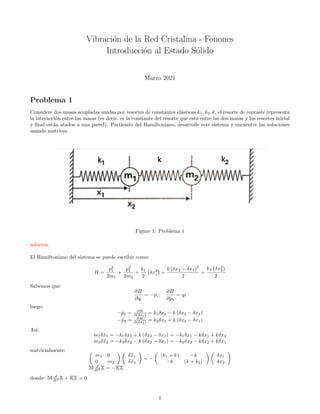
1. Vibración de la Red Cristalina - Fonones Introducción al Estado Sólido Marzo 2021 Problema 1 Considere dos masas acopladas unidas por resortes de constantes elásticas k1, k2, k, el resorte de contaste representa la interacción entre las masas (es decir, es la constante del resorte que está entre las dos masas y los resortes inicial y final están atados a una pared). Partiendo del Hamiltoniano, desarrolle este sistema y encuentre las soluciones usando matrices. Figure 1: Problema 1 solución El Hamiltoniano del sistema se puede escribir como: H = p2 1 2m1 + p2 1 2m2 + k1 2 δx2 1 + k (δx2 − δx1) 2 2 + k2 δx2 2 2 Sabemos que: ∂H ∂qi = − ˙ pi; ∂H ∂ps = qi luego: −ṗ1 = ∂H ∂(δx1) = k1δx1 − k (δx2 − δx1) −ṗ2 = ∂H ∂(δx2) = k2δx2 + k (δx2 − δx1) Ası́: m1δẍ1 = −k1δx1 + k (δx2 − δx1) = −k1δx1 − kδx1 + kδx2 m2δẍ2 = −k2δx2 − k (δx2 − δx1) = −k2δx2 − kδx2 + kδx1 matricialmente: m1 0 0 m2 δẍ1 δẍ2 = − (k1 + k) −k −k (k + k2) δx1 δx2 M d dt2 X = −KX donde: M d dt2 X + KX = 0 1

2. suponiendo una solución de la forma δx1 = A1 sin(ωt + ϕ); δx2 = A2 sin(ωt + ϕ) siendo A1 A2 las amplitudes de movimiento armónico, y ω frecuencias angulares. Reemplazando estas soluciones en M d dt2 X + KX = 0, se tiene: ∂2 (δx1) ∂t2 = −A1ω2 sin(ωt + ϕ) ∂ (δx2) ∂f2 = −A2ω2 sin(ωt + φ). −m1A1ω2 = −k1A1 − kA1 + kA2 → −A1ω2 = −−(k1+k)A1 m1 + k m1 A2 −m2A2ω2 = −k2A2 − kA2 + kA1 → −A2ω2 = −(k2−k)A2 m2 + k m2 A1 A1 −m1ω2 + k1 + k − kA2 = 0 A2 −m2ω2 + k2 + k − kA1 = 0 k1 + k − m1w2 −k −k k2 + k − m2ω2 A1 A2 = 0 Para hallar los valores ω que cumplan con la condición anterior, se debe hallar el determinante de la matriz:

6. k1 + k − m1ω2 −k −k k2 + k − m2ω2

10. = 0 k1 + k − m1ω2 k2 + k − m2ω2 − k2 = 0 m1m2ω4 − k1m2ω2 − km2ω2 − km1ω2 − k2m1ω2 + (k1 + k) (k2 + k) − k2 = 0 = (m1m2) ω4 − ω2 (k1m2 + km2 + km1 + k2m1) + (k1 + k) (k2 + k) − k2 = 0 haciendo ω2 = ω0 = (m1m2) ω02 − ω0 (m1 (k + k2) + m2 (k + k1)) + (k1 + k) (k2 + k) − k2 = 0 Ası́ las cosas: ω2 = m1 (k + k2) + m2 (k + k1) 2m1m2 ± q [m1 (k1 + k2) + m2 (k + k1)] 2 − 4 (m1m2) [(k1 + k) (k2 + k) − k2] 2m1m2 Problema 2 Desarrolle el problema de osciladores armónicos cuánticos acoplados aplicados a un sólido cristalino. solución Consideremos un sistema de N partı́culas de masa m conectadas mediante resortes de constante c y longitud natural a. Ahora bien, para que las condiciones de contorno sean periódicas, supondremos que las partı́culas forman un anillo. Si el desplazamiento de la particula s es qs y su momento lineal es ps, el Hamiltoniano del sistema está dado por: H = n X s=1 p2 s 2m + c 2 (qs+1 − qs) 2 El Hamiltoniano de oscilador armónico cuántico es: H = p2 2m + c 2 x2 Los valores de la energı́a para el nivel n-ésimo son: En = n + 1 2 ~ω n = 1, 2, 3, . . . se hará transformada de Fourier de las coordenadas ps y qs a las coordenadas PK y QK, conocidas como coordenadas de fonones; ası́ que QK = N−1/2 X s qse−iKsa 2

11. Por la condicion de contorno qs = qs + N lleva K = 2πn Na ; n = 0, ±1, ±2, . . . , ± 1 2 N − 1 , ± 1 2 N La transformada para Ps es PK = N−1/2 X s eiKsa Se debe comprobar que la transformada anterior es canónica. Usando el conmutador entre QK, PK0 [QK, P0 K] = N−1 X r qre−iKra , X s pseiK0 sa # = N−1 X r X S [qr, ps] e−ia(Kr−K0 s) Teniendo presente que, como q y p son variables conjugadas, entonces: [qr, ps] = i~δrs Ası́ se tendrá entonces: [QK, PK0 ] = N−1 i~ X r e−i(K−K0 )ra = N−1 i~ X r exp i2π (n0 − n) r N La expresión para el delta de Kronecker es: δn,n0 = 1 N PN `=1 exp 2πi N (n0 − n) Ası́ [QK, PK0 ] = i~δn,n0 = i~δK,K0 Por lo que QK y PK son variables conjugadas. Las transformadas inversas para psy qs son qs = N−1/2 P K QKeiKsa ps = N−1/2 P K PKe−iKsa De modo que: X S p2 s = N−1 X s X K X K0 PKPK0 e−i(K+K0 )sa = X K X K0 PKPKδ (−K, K0 ) = X K PKP−K y para qs: X s qs+1 − q2 s = N−1 X s X K X K0 QKQK0 h eiKa(s+1) − eiKsa i h eiK0 a(s+1) − eiK0 sa i = N−1 X S X K X K0 QKQr0 h eia(s+1)(K+K0 ) + eisa(K+K0 ) − eiKas+iKa+iK0 sa − eiKas+iK0 a+iK0 sa i = N−1 X s X K X K0 QKQK0 h NδK,−K0 + NδK,−K0 − eias(K+K0 )eiKa − eias(K+K0 )eiK0 a i = N−1 X K X K0 QKQK0 h NδK,−K0 + NδK,−K0 − NδK,−K0 eiKa − NδK,−K0 eiK0 a i = X K QKQ−K 1 + 1 − eiKa − e−iKa = X K QKQ−K 2 − (eiKa + e−iKa ) 3

12. = X K 2QKQ−K [1 − cos(Ka)] Ası́, el Hamiltonano H = Pn s=1 h p2 s 2m + c 2 (qs+1 − qs) 2 i queda expresado como: H = X k 1 2m PKP−K + CQKQ−K (1 − cos (Ka)} haciendo: ωK = 2c m 1 2 (1 − cos(Ka))1/2 entonces H = X K 1 2m PKP−K + 1 2 mω2 KQKQ−K haciendo uso de la mecánica cuántica i~Q̇K = [QK, H] = i~P−K m i~Q̈K = h Q̇K, H i = 1 m [P−K, H] = i~ω2 KQK luego: Q̈K + ω2 KQK = 0 (Ec. oscilador armónico con frecuencia ωK ) Enk = nK + 1 2 ~ωK ; nK = 0, 1, 2, 3, . . . La energı́a de todo el sistema será U = X k nK + 1 2 ~ωK En mecanica cuantica se tiene n̂k = â+ k âk, por lo tanto H = X k a+ k ak + 1 2 con: a+ |ni = √ n + 1|n + 1i a|ni = √ n|n − 1i y ror tanto: a+ a|ni = a+ √ n|n − 1i = n|ni aa+ |ni = a √ n + 1|n + 1i = (n + 1)|ni luego a, a+ = aa+ − a+ a = 1 Para probar que el Hamiltniano se puede expresar como estos operadores, se emplea el procedimiento anterior, ası́: QK = q ~ 2mωK aK + a+ −K PK = i q ~mωk 2 a+ K − a−K y ası́ qs = X k ~ 2NmωK 1 2 aKeiKs + a+ Ke−iKs También se tiene que: Q+ −k = QK ; P+ K = P−K Como ˆ qs y ˆ ps, y son operadores hermı́ticos: 4

13. qs = q+ s ; ps = p+ s y ası́ tenemos que [aK, aK + ] = 1 2~ mωK [QK1 , Q−K] − i (QK, PK] + i [P−K, Q−K] + [P−K, PK] · 1 mωK y como [QK, PK0 ] = i~δK,K0 , entonces aK, a+ K0 = δK,K0 Ası́ pues, otra forma de expresar la energı́a es: ~ωK a+ KaK + a+ −Ka−K = 1 2m (PKP−K + P−KPK) + 1 2 mω2 K (QKQ−K + Q−KQK) Problema 3 Desarrolle la dispersión elástica mediante fonones. Es decir, demuestre que cuando se crea un fonón de vector de onda k mediante la dispersión inelistica de un fotón o neutrón desde un vector de onda k al k, la regla de selección del vector de onda que gobiema el proceso es: k = k0 + K + G solución Partiendo de la cantidad de movimiento p = M d dt P us; cuando el cristal transformado lleva un fonón p = mdu dt P s eiska = M du dt P s e(ika)s . Tomando x = eika , se tiene que PN−1 s=0 xs = 1−xN 1−x . Por lo tanto p = M du dt 1 − eiNka 1 − eika siendo k = ±2πr Na , donde r ∈ Z ⇒ eiNka = e±i2πr = 1. Lo que lleva a que la cantidad de movimiento p = m du dt X s eiska = 1 − 1 1 − eika = 0 desde que se tiene momento atómico neto igual a 0 (P = 0), los fonones asociados tampoco podrán tener cantidad de movimiento. El vector de onda debe seguir la regla: k = k0 + k∗ si el vector de donde del fonón k∗ está fuera de la primera zona de Brillouin, se puede reemplazar k∗ por su equiv- alente dentro de la primera zona de Brillouin. k∗ − k = G ⇒ k∗ = k + G lo que significa que la red prefiere transferir la energı́a extra y el movimiento del cristal completo siempre que esté permitido. Dado que la energı́a de retroceso del cristal es despreciable, el cambio de la energı́a del neutrón viene solamente de la creación del fonón, y la energı́a de todas las partı́culas se conserva. ~ωk = ~ωk0 + ~ωk∗ ~ωk = ~ωk0 + ~ω(K + G) k = k0 + K + G 5

14. Problema 4 Encuentre el calor especifico para un conjunto de osciladores armónicos tridimensionales clásicos desacoplados (Ley de Doulong-Petit) solución Considerando un conjunto de N osciladores clásicos desacoplados podemos encontrar la energı́a promedio Ē para cada oscilador y obtener la energı́a total como Ē = ĒN. La capacidad calorı́fica se puede obtener luego como CV = ∂Ē ∂T V Considerando el Hamiltoniano de un oscilador H = ~ p2 2m + k 2 ~ x2 La función de partición clásica es z = 1 (2π~)3 R e−βH d~ xd~ p = 1 (2π~)3 RRRR RR ∞ −∞ e−β(p2 x+P 2 y +P 2 z ) 1 2m e−β(x2 +y2 +z2 )k 2 dxdydzdPkdPydPt = 1 (2πh)3 hq 2mπ β q 2π βk i3 = 1 ~ω β 3 = (~ωβ)−3 donde hemos usado que R ∞ −∞ e−αx2 dx = pπ α recordando que la frecuencia del oscilador es ω = p k/m. La energı́a promedio del oscilador la calculamos de la función de partición como Ē = − 1 z ∂z ∂β = −(~ωβ)−3 (−3) (~ωβ)3 · 1 β = 3 β = 3KBT Luego, la energı́a total es Ē = ĒN = 3NKBT y la capacidad calorı́fica del solido es C = ∂Ē ∂T = 3NKB Problema 5 Explicar los procesos Unklapp y hacer el respectivo desarrollo de los términos anarmónicos del potencial, en un cristal periódico. solución Figure 2: Ilustración problema 5 En el scattering de fonones, dos (o más) de estos pueden interactuar para crear otro fonón, si los vectores de anda son ~ k1,~ k2 para los fonones que interactúan y ~ k3 para el que se obtiene después de la interacción, por conservación del momento se tiene ~ k1 + ~ k2 = ~ k3 6

15. Figure 3: Representación de proceso normal y proceso Unklapp Sin embargo, si los fonones tienen una energı́a alta ( N 1 2 kBθ), con θ la temperatura de Debye, puede ocurrir que ~ k1 + ~ k2 este fuera de la primera zona de Brillouin en el espacio de los ~ k, en este caso se tiene ~ k1 + ~ k2 = ~ k3 + G con ~ G un vector de la red reciproca. Estos procesos con ~ G 6= − → 0 se llaman procesos Umklapp. Aunque en esta última ecuación no se conserva el momento, la energı́a se sigue conservando (ω1 + ω2 = ω3) . Problema 6 Explique cómo los términos anarmónicos llevan a la definición de la conductividad térmica en un sólido cristalino y realice los respectivos desarrollos. solución El coeficiente de conductividad térmica k en un sólido se define como Ju = −k dT dx con dT/dx el gradiente de temperatura y Ju la energı́a transmitida por unidad de área y por unidad de tiempo. La transferencia de energı́a es un proceso aleatorio que depende de la dispersión de los fonones en la red por lo que es necesario conocer el camino libre medio l de los fonones en el cristal l depende del scattering geométrico y del scattering entre fonones ( si T aumenta, habrá mas fonones en los modos excitados y el scatteripg entre fonones será mayor luego l ∝ 1 T ). Considerando en un sólido, la transferencia de energı́a en la dirección x, el flujo de particulas es n hvxi con n = #Fotones Volumen . Si c es la capacidad calorı́fica de la partı́cula al ir de un extremo a temperatura T + ∆x a otro a temperatura T, la partı́cula cederá una energı́a c∆T. Como ∆T = dT dx lx = dT dx vxτ con τ como el tiempo promedio entre colisiones. El flujo de energı́a es Ju = −n hvxi C∆T = −n v2 x Cτ dT dx = − 1 3 n v2 Cτ dT dx como l = vτ y la capacidad calorı́fica total por unidad de volumen es C = nc, se tiene Ju = − 1 3 Cvl dT dx luego k = 1 3 Cvl Problema 7 Mostrar que el coeficiente de expansión usando mecánica estadistica clásica está dado por: α = 1 L dL dT ≈ 1 x0 dhxiβ dT = 1 x0 kBκ3 κ2 7

16. Supongan que el potencial es de la forma: V (x) = κ 2 (x − x0) 2 − κ3 3! (x − x0) 3 + · · · Halle el valor esperado de x y expanda el potencial en exponenciales (explique por qué puede hacer esto) y use esto para obtener el coeficiente de expansión térmica. ¿Para qué rango de temperaturas es válida esta expresión de α ? ¿Este modelo de expansión térmica en un sólido es válido para el caso de una cadena de muchos átomos? solución (a) En mecánica estadı́stica clásica el valor esperado de x se obtiene como hxiβ = R xe−βV (x) dx R e−βV (x)dx donde e−βV (x) = e−β k 2 (x−x0)2 +β k3 6 (x−x0)3 +··· = e−β k 2 (x−x0)2 eβ k3 6 (x−x0)3 +··· Si el término cuadrático es dominante i.e. el término cúbico y 105 siguientes son pequeños comparados con este, podemos aproximar e−βV (x) = e−β k 2 (x−x0)2 1 + β k3 6 (x − x0) 3 + · · · Calculamos ahora hxiβ con esta aproximación hxiβ = R ∞ −∞ xe−β k 2 (x−x0)2 h 1 + β k3 6 (x − x0) 3 i dx R ∞ −∞ e−β k 2 (x−x0)2 h 1 + β k3 6 (x − x0) 3 i dx sea a = βk/2 y b = βk3/6 se tiene. Z ∞ −∞ xe−α(x−x0)2 h 1 + γ (x − x0) 3 i dx = x0 r π a + 3 4 r π a b a2 y Z ∞ −∞ e−α(x−x0)2 h 1 + γ (x − x0) 3 i dx = r π a luego hxiβ = x0 pπ a + 3 4 pπ a b a2 pπ a = x0 + 3 4 βk3 6 4 β2k2 = x0 + k3 2βk2 = x0 + kBk3T 2k2 Por lo tanto, α = 1 x0 dhxiT dT = 1 x0 kBk3 2k2 Para que el primer termino del potencial sea dominante β k 2 (x − x0) 2 ∼ 1 luego |x − x0| ∼ r kBT K además k |x − x0| 2 k3 |x − x0| 3 k k3 |x − x0| luego k2 k2 3 kBT k → 1 kB k3 k2 3 T → 1 kB ∼ 1023 Kelvin J , suponiendo k del orden de kB T 1023 Kelvin. (b) Para el caso de una cadena de muchos átomos este modelo podrı́a dar una buena aproximación para el coeficiente de expansión α, pero en general, es inválido. 8

17. Problema 8 solución (a) Muestre que la energı́a interna U de un sistema de partı́culas, puede ser escrita como U = − ∂ ln Z ∂β Donde β = 1/kBTi La distribución de probabilidad para cualquier variable α para una partı́cula está dada por: PT (α) = e−βEα P α e−βEα ; β = 1/KBT siendo P α e−βEα = Z(β) llamada función de partición, la cual nos normaliza la distribución de probabilidad PT (α). Ahora bien, el promedio de la energı́a esta dado por la sumatoria de la energı́a de cada estado por su respectiva probabilidad: hUi = X α EαPT (α) = X Eα e−βEx P α e−βEα }Z = 1 Z X α Eαe−βEα ello conlleva a: X α Eαe−βEα = − ∂ ∂β X a e−βEα ! = − ∂ ∂β (Z) por lo tanto hUi = − 1 Z ∂Z ∂β = − ∂ ln(Z) ∂β (b) Calcule CV = ∂U ∂T CV = ∂ ∂T − ∂ ln(Z) ∂β = − ∂ ∂T 1 Z ∂Z ∂β = − ∂ ∂T 1 P α e−βEα hX −Eαe−βEα i = ∂ ∂T P α Eαe−βEα P α e−βEα = ∂ ∂T P Eαe−βEα · P e−βEα − P Eαe−βEα ∂ ∂T P e−βEa [ P e−βEα ] 2 = − P E2 αe−βEα ∂β ∂T · P e−βEα − P Eαe−βEα · − P Eae−βEα ∂β ∂T [ P e−βEα ] 2 como ∂β ∂T = − 1 KBT 2 : CV = 1 [ P e−βEα ] 2 · X E2 αe−βEα · 1 KBT2 · X e−βEα − X Eαe−βEα · X Eαe−βEα · 1 KBT2 = 1 KBT2 · 1 Z2 X E2 αe−βEα · Z − X Eαe−βEα 2 = 1 kBT2 P E2 αe−βEα · Z Z2 − P Eαe−βEα 2 Z2 # = 1 kBT2 P E2 ae−βEα Z − P Eαe−βEα 2 Z2 # 9

18. teniendo presente que P E2 2 e−βEα Z = U2 , y que P Eαe−βEα Z = hUi; se tendrá: CV = 1 KBT2 U2 − hUi2 = KB KB 1 KBT2 U2 − hUi2 = KB (KBT) 2 U2 − hUi2 CV = KBβ2 U2 − hUi2 siendo σ2 = U2 − hUi2 la varianza de la energı́a interna del sistema. Extendiendo el resultado a 3 dimensiones y N partı́culas: CV = 3NKBβ2 σ2 U Problema 9 El argón es un cristal FCC que se caracteriza por tener enlaces tipo fuerzas de Van der Waals, para el cual el potencial de pares de átomos es del tipo Lennard-Jones: V (r) = 4ε σ r 12 − σ r 6 Donde ε = 1.05 × 10−2 eV y σ = 3.4Å. Despreciando todas las fuerzas de los vecinos cercanos, calcule la función de dispersión ω(k) para los fonones longitudinales en la dirección (1, 0, 0). solución El potencial de Lennard-Jones está dado como: V (r) = 4ε σ r 12 − σ r 6 Primero encontraremos d valor mı́nimo de “r” para después expandir en series de Taylor: dV (r) dr = 4ε −12 σ12 r13 + 6 σ6 r7 = 24ε r −2 σ r 12 + σ r 6 luego: dV (r) dr = 0 cuando 2 σ r 12 = σ r 6 con r0 = 21/6 σ V (r0) = −ε Para expandir V (r) en series de Taylor se debe hacerlo al rededor de r0, pero haciendo cambio de variable x = r−r0, expandindo alrededor de cero; haciendo V (r) → U(x) U(x) = U(0) + x dU ∂x

22. x=0 + x2 2 d2 U dx2

26. x=0 = −ε + 0 + 1 2 cx2 ası́: F = −∂U ∂x = −cx donde, para un átomo interactuando con otro: mẍ = −cx 10

27. Figure 4: Problema 9 quiere decir que, tomando en cuenta el átomo anterior y el siguiente, para la interacción del átomo de la mitad; entonces, se tiene: m d2 (δxn) dt2 = c (δxn+1 + δxn−1 − 2δxn) Donde se supondrá δxn = Ae−i~ kxeq n +iωt ; con xeq = na −ω2 me−i~ kna eiwt = c e−i~ kna eiωt e−i~ ka + e−i~ kna eiωt eika − 2e−i~ kna eiωt ω2 = −ω2 0 e−ika + eika − 2 ; con ω2 0 = c/m = −ω2 0(2 cos(ka) − 2) ω2 (k) = 2ω2 0(1 − cos(ka)) → Relación de dispersión = 4ω2 0 sin2 ka 2 Debido a que el análisis se hace sobre una estructura cúbica: d p h2 + K2 + l2 = α Para (h, k, l) =(1, 0, 0) → a = d adicional, se tiene que c = d2 U(x) dx2

31. x=0 = 4ε 12 · 13 σ12 r14 0 − 6.7 σ6 r8 0 Reemplazando el valor de r0 = 21/6 σ, llegamos a: c = 36ε 22/3σ2 ; ε = 1.05 × 10−2 eV ; σ = 3.4Å Ası́, la relación de dispersión será ω2 (k) = 4 c m sin2 kd 2 = 4 36ε 22/3σ2m sin2 Kd 2 = 2 × 6 21/3σ r ε m sin kd 2 ω2 (k) = 12 21/3σ r ε m sin kd 2 con ε = 1.05 × 10−2 eV, σ = 3.4Å, r0 = 21/6 σ Ahora bien, como es una red FCC; 11

32. Figure 5: Estructura FCC con 2r0 = √ 2d d = √ 2r0 d = 21/2 21/6 σ d = 22/3 σ entonces ω(k) = 12 21/3σ p ε m sin k(22/3 )σ 2 ω(k) = 12 21/6r0 p ε m sin kr0 21/2 ω(k) = 12 21/6r0 r ε m sin kr0 21/2 Problema 10 Una monocapa de gas se deposita en una superficie atómicamente perfecta (ninguna imperfección), considere primero un modelo en el cual el efecto de la superficie es simplemente confinar el movimiento de los átomos del gas al plano z = 0. Los átomos forman una red cuadrada, con a = 3Å. Para k = (kx, ky) pequeño, la ecuación de movimiento está dada por: −mω2 ei(k) = −A k2 x + k2 y ei(k) i = x, y Encuentre la densidad de estados normalizada, por unidad de frecuencia, cerca a ω = 0. solución Densidad de estados normalizada por uidad de frecuencia para pequeñas oscilaciones de red 2D Figure 6: Estructura cristalina Problema 10; red cuadrada, a = 3Å 12

33. La ecuación de movimiento es m d2 U dt2 = − c1 [2U(na, ma) − U ((n + 1)a, ma − U((n − 1)a, ma)] −c2 [2U(na, ma) − U (na, (m + 1)a) − U (n1, (m − 1)a)] con U = U(na, ma). Donde el lado derecho de la ecuación representa la fuerza que siente cada átomo, y se consideran interacciones únicamente inmediatos por cada fila y columna. n, m se consideran enteros, y U(na, ma) representa el desplazamiento respecto de la posición de equilibrio para el átomo (n, m). Si se propone una solución periódica de la forma U (na, ma) = Aeikxna+kyma−ωt resultarán soluciones de la forma ω2 = 4c1 m sen2 kxa 2 + 4c2 m sen2 kya 2 Por otro lado, la densidad de estados es igual al cambio del número de modos (número de átomos) normales respecto del cambio de frecuencia D(ω)dω = dN dω dω y el número de modos normales es igual a la dimensión de la celda en el espacio recı́proco por el área del cı́rculo de radio |k| Figure 7: Cı́rculo de radio |k| N = a 2π 2 × Área cı́rculo N = a 2π 2 πk2 N = A 4π2 π2 k2 N = Ak2 4π = a2 k2 4π Reemplazando en D(ω)dω = dN dω dω, resulta: D(ω)dω = dN dω dω = d dω a2 k2 4π dω = dk dω d dk a2 k2 4π dω = a2 4π (2π) dk dω dω = a2 2π kdk dω dω D(ω)dω = a2 2π µ dω/dk dω → gradiente →

35. ∇kω(k̄)

40. ~ Vg

43. |{z} Velocidad de grupo 13

44. Hallando dω dk desde ω2 = 4c1 m sen2 kxa 2 + 4c2 m sen2 kya 2 , se llega a: 2ω dω dk =

48. ∇ki 4c1 m sen2 kxa 2 + 4c2 m sen2 kya 2

56. ∇ki 4c1 m sen kxa 2 cos kxa 2 + 4c2 m sen kya 2 cos kya 2

70. ∇ki       4c1 m sen kxa 2 cos kxa 2 | {z } sen(kxa) 2 + 4c2 m sen kya 2 cos kya 2 | {z } sen(kya) 2      

80. = 4a m s c2 1 4 sen2(kxa) + c2 2 4 sen2 (kya) 2ω dω dk = 2a m q [c2 1 sen2(kxa) + c2 2 sen2 (kya)] dω dk = a mω q c2 1 sen2 (kxa) + c2 2 sen2 (kya) reemplazando en D(ω)dω = a2 2π µ dω/dk dω D(ω)dω = a 2 2π · Kdω · 1 a mω p c2 1 sen2 (kya) + c2 sen2 (kya) D(ω)dω = amωK 2π p c2 1 sen2 (kxa) + c2 2 sen2(kya) dω La cual representa la densidad de estados por unidad de frecuencia para pequeñas oscilaciones de una red bidimen- sional cuadrada de un gas monoátomico. 14

Ejercicios vibacion de red cristalina

Empfohlen

Empfohlen

Weitere ähnliche Inhalte

Was ist angesagt?

Was ist angesagt? (20)

Ähnlich wie Ejercicios vibacion de red cristalina

Ähnlich wie Ejercicios vibacion de red cristalina (20)

Mehr von CA BE

Mehr von CA BE (7)

Kürzlich hochgeladen

Kürzlich hochgeladen (20)

Ejercicios vibacion de red cristalina