Geometria analitica
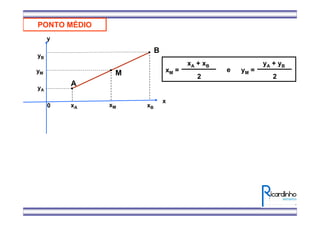
- 1. B A M xBxMxA yB yM yA x y xM = xA + xB 2 yM = yA + yB 2 e 0 PONTO MÉDIO
- 2. x y xC yA A B C xA xB yB yC BARICENTRO DE UM TRIÂNGULO MM11 MM22 MM33 GG xG = xA + xB + xC 3 yM = yA + yB + yC 3 e Calcule as coordenadas do baricentro de um triângulo ABC,Calcule as coordenadas do baricentro de um triângulo ABC, sabendo que ADsabendo que AD éé uma de suas medianas e que A(uma de suas medianas e que A(--5, 8) e D(1,5, 8) e D(1, --1).1). a) (0, 2) b) (a) (0, 2) b) (--1, 2) c) (2,1, 2) c) (2, --1) d) (1) d) (--1, 1) e) (2,1, 1) e) (2, --2)2)
- 3. x y xC yA A B C xA xB yB yC ÁREA DE UM TRIÂNGULO 1yCxC 1yBxB 1yAxA A = 1 2 x y 4 1 A B C 2 6 3 5 ③③③③ ①①①① ②②②② M NP AT = AMNP – (AT1 + AT2 + AT3)
- 4. EXERCÍCIOS ( UFPR – 2012 ) Calcule a área do quadrilátero P1P2P3P4 , cujas coordenadas cartesianas são dadas na figura abaixo.
- 5. ( FURG-RS ) Os pontos (1,3), (2,7) e (4,k) do plano cartesiano estão alinhados se e somente se: a) k = 15 b) k = 11 c) k = 14 d) k = 12 e) k = 13
- 6. B A M xBxMxA yB yM yA x y xM = xA + xB 2 yM = yA + yB 2 e 0 PONTO MÉDIO x y xC yA A B C xA xB yB yC ÁREA DE UM TRIÂNGULO 1yCxC 1yBxB 1yAxA A = 1 2
- 7. DISTÂNCIA ENTRE DOIS PONTOS A B xA xB yA yB x y 0 (dAB)2 = (xB – xA)2 xB – xA yB – yA + (yB – yA)2 2 AB 2 ABAB )y(y)x(xd −+−= ( UFRGS - 08 ) Sendo os pontos A (– 1, 5) e B(2, 1) vértices consecutivos de um quadrado, o comprimento da diagonal desse quadrado é
- 8. ESTUDO DO PONTO 2 AB 2 ABAB )y(y)x(xd −+−= x x x M A B = + 2 y y y M A B = + 2 ( UFPEL ) Na arquitetura, a matem( UFPEL ) Na arquitetura, a matemááticatica éé usada ausada a todo momento. A geometriatodo momento. A geometria éé especialmenteespecialmente necessnecessáária no desejo de projetos. Essa parte daria no desejo de projetos. Essa parte da MatemMatemáática ajuda a definir a forma dos espatica ajuda a definir a forma dos espaçços,os, usando as propriedades de figuras planas eusando as propriedades de figuras planas e ssóólidas. Ajuda tamblidas. Ajuda tambéém a definir a medidas dessesm a definir a medidas desses espaespaçços. Uma arquitetaos. Uma arquiteta éé contratada para fazer ocontratada para fazer o jardim de uma residência, que deve ter o formatojardim de uma residência, que deve ter o formato triangular. Analisando a planta baixa, verificatriangular. Analisando a planta baixa, verifica--sese que os vque os véértices possuem coordenadasrtices possuem coordenadas A(8,4);A(8,4); B(4,6); C(2,4). No ponto mB(4,6); C(2,4). No ponto méédio do lado formadodio do lado formado pelos pontos A e Cpelos pontos A e C éé colocado um suporte paracolocado um suporte para luminlumináárias. Considerando o texto e seusrias. Considerando o texto e seus conhecimentos,conhecimentos, éé correto afirmar que a distânciacorreto afirmar que a distância do suporte atdo suporte atéé o ponto B mede, em unidades deo ponto B mede, em unidades de comprimento.comprimento. 17e) 13d) 5c) 3b) 37a)
- 9. ESTUDO DO PONTO 2 AB 2 ABAB )y(y)x(xd −+−= x x x M A B = + 2 y y y M A B = + 2 ( UFPR( UFPR –– 2011 ) Durante um passeio, uma2011 ) Durante um passeio, uma pessoa fez o seguinte trajeto: partindo de umpessoa fez o seguinte trajeto: partindo de um certo ponto, caminhou 3 km no sentido norte,certo ponto, caminhou 3 km no sentido norte, em seguida 4 km para o oeste, depois 1 km noem seguida 4 km para o oeste, depois 1 km no sentido norte novamente, e então caminhou 2sentido norte novamente, e então caminhou 2 km no sentido oeste. Apkm no sentido oeste. Apóós esse percurso, as esse percurso, a que distância a pessoa se encontra do pontoque distância a pessoa se encontra do ponto de onde iniciou o trajeto?de onde iniciou o trajeto?
- 10. ESTUDO DO PONTO 2 AB 2 ABAB )y(y)x(xd −+−= x x x M A B = + 2 y y y M A B = + 2 ( UFRGS( UFRGS –– 2013 ) Considere os gr2013 ) Considere os grááficos dasficos das funfunçções f e g, definidas por f(x) = xões f e g, definidas por f(x) = x22 + x+ x –– 2 e2 e g(x) = 6g(x) = 6 –– x, representadas no mesmo sistemax, representadas no mesmo sistema de coordenadas cartesianas, e os pontos A e B,de coordenadas cartesianas, e os pontos A e B, intersecintersecçção dos grão dos grááficos das funficos das funçções f e g,ões f e g, como na figura abaixo.como na figura abaixo. A distância entre osA distância entre os pontos A e Bpontos A e B éé:: 26e) 25d) 24c) 23b) 22a)
- 11. ESTUDO DO PONTO 2 AB 2 ABAB )y(y)x(xd −+−= x x x M A B = + 2 y y y M A B = + 2 Seja uma circunferência cujo centro pertenceSeja uma circunferência cujo centro pertence ao eixo das abscissas e os pontos (2, 2) e (8,4)ao eixo das abscissas e os pontos (2, 2) e (8,4) as extremidades de uma de suas cordas. Aas extremidades de uma de suas cordas. A áárea da superfrea da superfíície limitada por essacie limitada por essa circunferência mede:circunferência mede:
- 12. ESTUDO DA RETA EQUAÇÕES DA RETA EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n Coef. angular Coef. linear FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos x y O 3 1 r 2 3 A B P(x, y) 133 121 1yx = 0 x + 3y + 6 – 3 – 3x – 2y = 0 – 2x + y + 3 = 0 geral y = 2x – 3 reduzida Coef. angular Coef. linear
- 13. ESTUDO DA RETA EQUAÇÕES DA RETA EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n Coef. angular Coef. linear FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos ( UDESC ) A soma do coeficiente angular( UDESC ) A soma do coeficiente angular com o coeficiente linear da reta quecom o coeficiente linear da reta que passa pelos pontospassa pelos pontos A(A(1,5) e1,5) e B(B( 4,14)4,14) éé::
- 14. ESTUDO DA RETA EQUAÇÕES DA RETA EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n Coef. angular Coef. linear FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos CÁLCULO DO COEFICIENTE ANGULAR B x y O yB yA xBxA A αααα (0, n) αααα yB– yA xB– xA r AB AB xx yy m − − = m = tg α ∆x ∆y m = Conhecendo 2 pontos Conhecendo a inclinação
- 15. CÁLCULO DO COEFICIENTE ANGULAR B x y O yB yA xBxA A αααα (0, n) αααα yB– yA xB– xA r AB AB xx yy m − − = m = tg α ∆x ∆y m = Conhecendo 2 pontos Conhecendo a inclinação x y O α A B –2 1 3 5 2)(1 35 m −− − = AB AB xx yy m − − = 3 2 m =
- 16. CÁLCULO DO COEFICIENTE ANGULAR B x y O yB yA xBxA A αααα (0, n) αααα yB– yA xB– xA r AB AB xx yy m − − = m = tg α ∆x ∆y m = Conhecendo 2 pontos Conhecendo a inclinação x y O α A B –2 3 3 –1 32 1)(3 m −− −− = AB AB xx yy m − − = 5 4 m −=
- 17. CÁLCULO DO COEFICIENTE ANGULAR B x y O yB yA xBxA A αααα (0, n) αααα yB– yA xB– xA r AB AB xx yy m − − = m = tg α ∆x ∆y m = Conhecendo 2 pontos Conhecendo a inclinação x y O 120º45º rt mr = tg 45º = 1 mt = tg 120º – √3= – tg 60º = 60º
- 18. CÁLCULO DO COEFICIENTE ANGULAR B x y O yB yA xBxA A αααα (0, n) αααα yB– yA xB– xA r AB AB xx yy m − − = m = tg α ∆x ∆y m = Conhecendo 2 pontos Conhecendo a inclinação CASOS PARTICULARES x y O A B –1 3 3 m = tg α m = tg 0° m = 0 EQUAÇÃO y = 3 x y O M N –1 2 3 m = tg α m = tg 90° m (não existe) EQUAÇÃO x = 2
- 19. ( UFRGS( UFRGS –– 2012 ) As equa2012 ) As equaçções das retas representadas no sistema deões das retas representadas no sistema de coordenadas cartesianas abaixo são:coordenadas cartesianas abaixo são: 2x + y2x + y –– 3 = 0, 5x3 = 0, 5x –– 4y4y –– 8 = 0 e x8 = 0 e x –– 3y + 3 = 0.3y + 3 = 0. As equaAs equaçções deões de rr ee ss são, respectivamente,são, respectivamente, a) 2x + ya) 2x + y –– 3 = 0 e x3 = 0 e x –– 3y + 3 = 0.3y + 3 = 0. b) 2x + yb) 2x + y –– 3 = 0 e 5x3 = 0 e 5x –– 4y4y –– 8 = 0.8 = 0. c) 5xc) 5x –– 4y4y –– 8 = 0 e x8 = 0 e x –– 3y + 3 = 0.3y + 3 = 0. d) xd) x –– 3y + 3 = 0 e 2x + y3y + 3 = 0 e 2x + y –– 3 = 0.3 = 0. e) xe) x –– 3y + 3 = 0 e 5x3y + 3 = 0 e 5x –– 4y4y –– 8 = 0.8 = 0.
- 20. ESTUDO DA RETA EQUAÇÕES DA RETA EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n Coef. angular Coef. linear FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos CÁLCULO DO COEFICIENTE ANGULAR AxBx AyBy m − − =m = tg α Dados 1 ponto e o coef. angular y – yo = m(x – xo) Encontrar a equação da reta r que passa pelos pontos A (10, 25) e B(15, 40) AxBx AyBy m − − = 1015 2540 m − − = m = 3 y – yo = m(x – xo) y – 25 = 3(x – 10) y – 25 = 3x – 30 y = 3x – 5 x y B 15 40 10 25 A
- 21. ( UFPR ) Sabe-se que a reta r passa pelos pontos A = (−2,0) e P = (0,1) e que a reta s é paralela ao eixo das ordenadas e passa pelo ponto Q = (4,2). Se B é o ponto em que a reta s intercepta o eixo das abscissas e C é o ponto de interseção das retas r e s, então o perímetro do triângulo ABC é: )3(5e) )33(3d) )5(3c) )33(5b) )53(3a) + + + + + 5 5
- 22. ( UFSC ) Calcular a área da região limitada pelas retas y = 5, 5x + 2y - 95 = 0, x = 0 e y = 0. GABARITO: 90
- 23. ESTUDO DA RETA EQUAÇÕES DA RETA EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n Coef. angular Coef. linear FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos CÁLCULO DO COEFICIENTE ANGULAR AxBx AyBy m − − =m = tg α Dados 1 ponto e o coef. angular y – yo = m(x – xo) ( UFRGS ) Os pontos A(-1,3) e B(5,-1) são extremidades de uma das diagonais de um quadrado. A equação da reta suporte da outra diagonal é: a) 2x - 3y - 1 = 0 b) 2x + 3y - 7 = 0 c) 3x + 2y - 8 = 0 d) 3x - 2y - 4 = 0
- 24. ( UFPR – 2011 ) Um balão de ar quente foi lançado de uma rampa inclinada. Utilizando o plano cartesiano, a figura ao lado descreve a situação de maneira simplificada. Ao ser lançado, o balão esticou uma corda presa aos pontos P e Q, mantendo-se fixo no ar. As coordenadas do ponto P, indicado na figura, são, então: a) (21,7). b) (22,8). c) (24,12). d) (25,13). e) (26,15).
- 25. ESTUDO DA RETA EQUAÇÕES DA RETA EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n Coef. angular Coef. linear FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos CÁLCULO DO COEFICIENTE ANGULAR AxBx AyBy m − − =m = tg α Dados 1 ponto e o coef. angular y – yo = m(x – xo) DISTÂNCIA ENTRE PONTO E RETA ( UFSC – 2010 ) Em um mapa de um deserto, localizado sobre um sistema de eixos cartesianos ortogonal, o faminto Coiote, cuja posição é dada pelo ponto P(1,2), vai tentar capturar o Papa-léguas, que se aproxima do Coiote descrevendo uma trajetória retilínea segundo a equação 3x + 4y = 31. A menor distância que o Coiote deve percorrer para capturar o Papa-léguas é de: RESPOSTA: 04
- 26. ESTUDO DA RETA EQUAÇÕES DA RETA EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n Coef. angular Coef. linear FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos CÁLCULO DO COEFICIENTE ANGULAR AxBx AyBy m − − =m = tg α Dados 1 ponto e o coef. angular y – yo = m(x – xo) DISTÂNCIA ENTRE PONTO E RETA ( UFSC ) Dados os pontos A(1, −−−−1), B(−−−−1, 3) e C(2, 7), determine a medida da altura do triângulo ABC relativa ao lado BC. RESPOSTA: 04
- 27. ESTUDO DA CIRCUNFERÊNCIA x y C αααα x y P ββββ x - αααα y - ββββ R EQUAÇÃO DA CIRCUNFERÊNCIA EQUAÇÃO REDUZIDA (x – αααα)2 + (y – ββββ )2 = R2 EQUAÇÃO GERAL x2 + y2 + Ax + By + C = 0 A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2 Determine as coordenadas do centro e o raio das circunferências: a) x2 + y2 – 4x – 6y - 12 = 0 b) x2 + y2 – 8x – 2y + 1 = 0 a) C (2, 3); R = 5 b) C (4, 1); R = 4
- 28. EQUAÇÃO DA CIRCUNFERÊNCIA EQUAÇÃO REDUZIDA (x – αααα)2 + (y – ββββ )2 = R2 EQUAÇÃO GERAL x2 + y2 + Ax + By + C = 0 A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2 Resposta: 12
- 29. EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n RETA - FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos AxBx AyBy m − − = m = tg α Dados 1 ponto e o coef. angular y – yo = m(x – xo) 2222bbbb2222aaaa ||||cccc PPPP b . y b . y b . y b . y PPPP a . x a . x a . x a . x |||| dddd + ++ = DISTÂNCIA ENTRE PONTO E RETA CIRCUNFERÊNCIA (x – αααα)2 + (y – ββββ )2 = R2 x2+y2+Ax+By+C = 0 A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2 RESPOSTA: 03
- 30. EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n RETA - FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos AxBx AyBy m − − = m = tg α Dados 1 ponto e o coef. angular y – yo = m(x – xo) 2222bbbb2222aaaa ||||cccc PPPP b . y b . y b . y b . y PPPP a . x a . x a . x a . x |||| dddd + ++ = DISTÂNCIA ENTRE PONTO E RETA CIRCUNFERÊNCIA (x – αααα)2 + (y – ββββ )2 = R2 x2+y2+Ax+By+C = 0 A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2 RESPOSTA: 18
- 31. EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n RETA - FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos AxBx AyBy m − − = m = tg α Dados 1 ponto e o coef. angular y – yo = m(x – xo) 2222bbbb2222aaaa ||||cccc PPPP b . y b . y b . y b . y PPPP a . x a . x a . x a . x |||| dddd + ++ = DISTÂNCIA ENTRE PONTO E RETA CIRCUNFERÊNCIA (x – αααα)2 + (y – ββββ )2 = R2 x2+y2+Ax+By+C = 0 A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2 ( FGV-SP ) A reta 3x + 4y - 6 = 0 determina na circunferência x2 + y2 – 2x – 4y + 1 = 0 uma corda de comprimento igual a:
- 37. EQUAÇÃO GERAL ax + by + c = 0 EQUAÇÃO REDUZIDA y = mx + n RETA - FORMAS DE OBTENÇÃO 0 1yx 1yx 1yx BB AA = Dados 2 pontos AxBx AyBy m − − = m = tg α Dados 1 ponto e o coef. angular y – yo = m(x – xo) 2222bbbb2222aaaa ||||cccc PPPP b . y b . y b . y b . y PPPP a . x a . x a . x a . x |||| dddd + ++ = DISTÂNCIA ENTRE PONTO E RETA CIRCUNFERÊNCIA (x – αααα)2 + (y – ββββ )2 = R2 x2+y2+Ax+By+C = 0 A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2 2 AB 2 ABAB )y(y)x(xd −+−= x y C αααα x y P ββββ x - αααα y - ββββ R DISTÂNCIA ENTRE 2 PONTOS EQUAÇÃO REDUZIDA EQUAÇÃO GERAL
- 38. POSIÇÕES RELATIVAS ENTRE DUAS CIRCUNFERÊNCIAS ( R > r) TANGENTES C1 C2 C1 C2 R rR d(C1, C2) = R + r r d(C1, C2) = R – r SECANTES C1 C2 R R – r < d(C1, C2) < R + r r NÃO SE INTERCEPTAM C1 C2 d(C1, C2) > R + r C1 C2 d(C1, C2) < R – r