El documento resume conceptos elementales de geometría, incluyendo fórmulas para calcular el perímetro y área de figuras básicas como triángulos, cuadrados, rectángulos, círculos y otros polígonos. También explica conceptos como ángulos, rectas paralelas, clasificación y propiedades de triángulos, y congruencia.

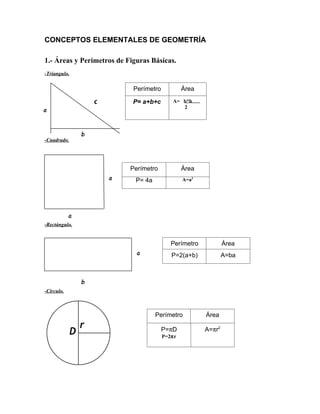
1. CONCEPTOS ELEMENTALES DE GEOMETRÍA
1.- Áreas y Perímetros de Figuras Básicas.
-Triangulo.
Perímetro Área
P= a+b+c A= b*h
2
-Cuadrado.
Perímetro Área
P= 4a A=a2
-Rectángulo.
Perímetro Área
P=2(a+b) A=ba
-Circulo.
Perímetro Área
P=πD A=πr2
P=2πr

2. -Trapecio.
Perímetro Área
P=a+b+c+d
-Rombo.
Perímetro Área
A= Dd
P=4a 2
-Pentágono.
Perímetro Área
A= Pa
P=5l 2
-Hexágono.
Área Perímetro
A= Pa
2 P=6l
2.- Propiedades de las Rectas paralelas.

3. -Ángulos exteriores (a, b, g, h).
-Ángulos interiores (c, d, e, f).
-Ángulos alternos internos ( c y f, e y d).
-Ángulos alternos externos ( b y g, a y h).
-Ángulos correspondientes (a y e, c y g, b y f, d y h).
-Ángulos opuestos por el vértice ( a y d, c y b, e y h, g y f)

4. Los triángulos y sus Propiedades.
a) Simbología de triángulos:
b) Clasificación de Triángulos:
1.-De acuerdo a sus lados: Equilátero, Isósceles, escaleno.
2.-De acuerdo a sus ángulos: Rectángulo, Oblicuo, Obtuso.
c) Área y Perímetro:
Teorema de Heron (conociendo sus lados)
S= Semiperimetro
d) Ángulos internos y externos de un triangulo.
La suma de los ángulos internos de un triangulo es igual a
180°.
La suma de los ángulos externos de un triangulo es igual a
900° .

5. Considerando un polígono como la composición de varios triángulos tenemos que la suma de los ángulos
internos de un polígono es igual a :
Siendo n el numero de vértices o lados. La suma de los ángulos externos de cualquier polígono es:
Siendo n el numero de ángulos o vértices.
Ejemplo:
Utilizando la formula
Para cualquier polígono:
Ejemplos sobre la demostración de un teorema: “dos ángulos opuestos por el
vértice son iguales”
Figura Hipótesis Tesis
X Los ángulos m y n son
m n opuestos por el vértice. ∠m = ∠n

6. RAZONAMIENTO
Afirmaciones Razones
∠m + ∠x = 180º Por ser adyacentes suplementarios.
∠n + ∠x = 180º Por la razón anterior.
∠m + ∠x = ∠n + ∠x Si los segundos miembros de dos
igualdades son iguales, los primeros
miembros también lo son. (propiedad
transitiva de la igualdad)
ANGULOS
Teorema: “la suma de los ángulos internos de un triángulo cualquiera es de
1800 ”
Figura Hipótesis Tesis
C
ABC : es un triángulo ∠A + ∠B + ∠C = 180O
cualquiera.
A B
Ángulo: es la amplitud de rotación que sobre un plano efectúa una semirrecta o
rayo manteniéndose fijo y como centro de la rotación el punto inicial de la semirrecta.

7. La semirrecta en la posición en que principia la rotación recibe el nombre de
lado inicial del ángulo, llamándose lado final o terminal del ángulo a la posición
adquirida por la semirrecta al final de su rotación. P
B
Ejemplos:
O A R Q
En el ∠ AOB, el lado AO es el lado inicial y el lado OB es el lado final o
terminal; en el ∠ PQR, PQ es el lado inicial y QR es el lado final o terminal.
Clasificación de los ángulos según su amplitud de rotación
 Agudo: si su amplitud es menor que un cuarto de vuelta; es decir, si mide menos
de 900
 Rectos: si su amplitud es de un cuarto de vuelta; es decir, si mide 900
 Obtuso: si su amplitud es mayor que un cuarto de vuelta y menor que media
vuelta; es decir, si mide más de 900 y menos de 1800
 Colineal o llano: si su amplitud es de media vuelta; es decir, si mide 1800
 Entrante: si su amplitud es mayor de media vuelta, más de 180 0 y menor que una
vuelta, menos de 3600
 Perigono: si su amplitud es de una vuelta; es decir, si mide 3600
B C D
O
O A O A O A E A
∠ AOB < 900 ∠ AOC = 900
∠ AOD > 90 y < 1800
0
∠ AOE = 180 0
AGUDO RECTO OBTUSO COLINEAL
O A
G
∠ AOG > 1800 y < 3600 ∠ AOA = 3600
ENTRANTE PERIGONO

8. Cómo se lee un ángulo
Si se emplean tres letras mayúsculas para designarlo, debe leerse en primer
término la letra colocada en el lado inicial, después la letra colocada en el vértice y
finalmente la letra correspondiente al lado terminal.
En ocasiones por necesidad resulta utilizar una sola letra mayúscula para
designar un ángulo, y ésta se coloca en el vértice del ángulo.
Ejemplos: B Y
∠ AOB ∠ XOY
O A O X
Ángulos adyacentes: son dos ángulos contiguos cuyos lados no comunes son
perpendiculares o están en línea recta. En el primer caso se les llama adyacentes
complementarios y en el segundo caso se les llama adyacentes suplementarios.
n
m q p
m + n = 900 p + q = 1800
Complemento de un ángulo: es lo que falta o sobra para medir un ∠ de 900
Suplemento de un ángulo: es lo que falta o sobra para medir un colineal ∠ de 1800
C B 890 59’ 60’’ 1790 59’ 60’’
Ejemplos: - 650 15’ - 650 15’ T
240 44’60’’ = complemento suplemento =1140 44’60’’
O A W R
El complemento del ∠ AOB es el ∠ BOC El suplemento del ∠ RST es el ∠ TSW
Suma de ángulos internos y externos de un polígono
El triángulo: es una superficie plana trilateral ; es decir, tiene tres lados y por lo
tanto tres ángulos y tres vértices.
Para designar un triángulo se emplea el símbolo ∆; para nombrarlo se pueden
usar tres letras de sus vértices en cualquier orden, o emplear una cifra romana que
se coloca en el interior del triángulo.
B
c I a
Ejemplo: A C
b

9. Clasificación de los triángulos
Según sus lados: C
 Triángulo escaleno: ninguno de sus lados es igual. A B
C
 Triángulo isósceles: dos de sus lados son iguales.
A B
C
 Triángulo equilátero: tiene sus tres lados iguales. A B
Según sus ángulos:
 Triángulo rectángulo: es el que tiene un ángulo recto, el lado opuesto al ángulo
recto se denomina hipotenusa, los lados perpendiculares al ángulo recto se
llaman catetos del triángulo rectángulo. C
A B
C
 Triángulo obtusángulo: es el que tiene un ángulo obtuso. A B
C
 Triángulo acutángulo: tiene tres ángulo agudos. A B
Rectas y puntos notables en un triángulo
Rectas:
 Mediana: segmento trazado desde un vértice hasta el punto medio del lado
opuesto.
 Mediatriz: perpendicular trazada en el punto medio de cada lado.
 Bisectriz: recta notable que corresponde a la bisectriz de un ángulo interior.
 Altura: perpendicular trazada desde un vértice, al lado opuesto o a su
prolongación. Hay tres alturas, una correspondiente a cada lado.
Propiedades de los triángulos

10.  La altura correspondiente a la base de un ∆ isósceles es también la mediana,
mediatriz y bisectriz de dicho triángulo.
 En dos ∆ congruentes, a ∠s congruentes se oponen lados congruentes y
viceversa.
 En todo ∆ un lado es menor que la suma de los otros dos y mayor que su
diferencia.
 En todo ∆ a mayor lado se opone mayor ∠ y viceversa.
 En dos triángulos que tienen dos lados respectivamente congruentes, y no
congruente el ∠ comprendido, a mayor ∠ se opone mayor lado.
Identificación de rectas y puntos en los triángulos
Mediana
Circuncentro
Baricentro
Mediatriz
Incentro
Bisectriz
Ortocentro Altura
Altura Altura Ortocentro
Altura Baricentro
Recta Euler
Ortocentro Circuncentro
EJERCICIOS

11. Resuelve los siguientes ejercicios:
1.- Hallar el valor en grados del ángulo X, sabiendo que la recta AB es perpendicular
a la recta CD en la siguiente figura.
A
E
X=
X 35 0
C D
B
2.- En la figura el ∠1 = 200 el ∠2 = 700 el ∠3 = 1400 , entonces el valor del ∠4 es:
3 ∠4 =
1
4 2
3.- En la figura el valor del ∠X es igual a:
650
X
450 500
Calcula el siguiente perímetro:
3X – 1
4.- 3X – 1 3X – 1 P=
3X –1

12. Calcula el área sombreada:
5.- 5a
3a 7b
1.- Determinar el área lateral, el área total y el volumen de un prisma triangular
recto que mide por lado en la base 6 cm., siendo la altura del prisma de 15 cm.
h = 15 cm
l = 6 cm
2.- Determinar el área lateral, el área total y el volumen de un cilindro circular recto
que mide de radio en su base 3 cm., y cuya altura es de 5 cm.
3 cm
h = 5 cm.
3.- Determinar el área lateral, área total y el volumen de un cono de revolución que
mide de radio 3 cm., de altura 4 cm., y cuya generatriz es consecuentemente de 5
cm.
g = 5 cm

13. h=4 cm
3 cm
CONGRUENCIA Y CUADRILÁTEROS
Congruencia
En geometría se requiere una definición apropiada para decidir cuándo dos
figuras, son congruentes.
Se llaman figuras congruentes aquellas que tienen la misma forma y el mismo
tamaño.
Aplicación del álgebra a los elementos homólogos de dos triángulos
congruentes
D C ∆I = ∆II, los ángulos correspondien
2X tes son iguales;
I 3Y 2x = 24 o X = 12;
3y = 60 ∴Y = 20
600 240 II
A B
D ∆I = ∆II, los lados correspondien
I tes son iguales;
X + 20 = 26 ∴X = 6;
A Y-5 260 C Y-5 = 42 ∴ Y = 47
420 X+ 200
II
B
Demostración de algunos teoremas sobre la congruencia en relación con
propiedades de ciertos triángulos.

14. El triángulo se define como una superficie plana trilateral; es decir tiene tres
lados, y por lo tanto tres ángulos y tres vértices, es el polígono con menos lados.
El contenido sobre la clasificación y las propiedades de los triángulos se
mencionan en la unidad Nº 1 de esta compilación matemática por lo tanto
pasaremos a plasmar algunos teoremas sobre la congruencia en relación con
propiedades de ciertos triángulos.
Teorema.- La suma de dos ángulos agudos de un triángulo rectángulo es igual a un
ángulo recto.
Hipótesis: Si ∠A, ∠C, ∠900 son tres ángulos del triángulo rectángulo, luego los
ángulos agudos son A y C.
C
Tesis: Entonces ∠A + ∠C = ∠ rectángulo = 900
Demostración: ∠A + ∠C + ∠900 = 1800 = 2∠ rectos
∠A + ∠C = 1800 - 900 = 900 = 1∠ rectángulo. A
Teorema.- Un ángulo externo de un triángulo es igual a la suma de los dos ángulos
internos que no le son adyacentes.
Hipótesis: en el ∆ ABC, ∠x = ángulo exterior.
∠A y ∠C son los ángulos interiores no adyacentes al ∠x C
Tesis: ∠x ≅ ∠A + ∠C
Demostración: ∠x + ∠B = 2∠ rectos A X
∠x = 2∠ rectos - ∠B (1) B
También: ∠A + ∠B + ∠C = 2∠ rectos
∴∠A + ∠C = 2∠ rectos - ∠B (2)
Comparando (1) con (2) se tienen dos cosas iguales a una tercera; son iguales ÷ sí.
∠x ≅ ∠A + ∠C

15. Demostración de algunos teoremas sobre la congruencia en relación con
propiedades de ciertos cuadriláteros.
Cuadrilátero se define como toda figura plana cerrada, limitada por cuatro
lados, en su tipología podemos mencionar el cuadrado, el trapecio, el rombo y el
paralelogramo.
Cuadrado Trapecio Isós. Rombo Paralelogramo Rectángulo Trapecio Rect.
• El cuadrado es un cuadrilátero que se caracteriza por tener sus cuatro lados
iguales y sus cuatro ángulos rectos.
• Se llama trapecio a un cuadrilátero que tiene dos sus lados paralelos. Es trapecio
rectángulo si uno de los lados no paralelos es perpendicular a las bases;
designándose con el nombre de trapecio isósceles aquel cuyos lados no paralelos
son iguales.
• El rombo es un cuadrilátero cuyos lados son iguales y paralelos dos a dos, siendo
iguales sus ángulos opuestos.
• El paralelogramo se caracteriza por ser un cuadrilátero cuyos lados opuestos son
paralelos.
• El rectángulo es un paralelogramo cuyos cuatro ángulos son rectos.
Propiedades del paralelogramo
 Sus lados opuestos son iguales.
 Sus ángulos opuestos son iguales.
 Sus diagonales se dividen mutuamente en partes iguales.
 Si sus diagonales son iguales, el paralelogramo es un rectángulo.
 Si sus diagonales son perpendiculares, el paralelogramo es un rombo.
 Los ángulos contiguos de un paralelogramo son suplementarios.
Teorema.- Los ángulos opuestos de un paralelogramo son congruentes y sus
ángulos contiguos son suplementarios.
D C
Dado: ∠A =∠C
∠B = ∠D
∠A+∠B = 1800 A E
B

16. Teorema.- Un paralelogramo es rombo si sus diagonales son perpendiculares.
D
Dado: ABCD es un rombo y un paralelogramo en el cual AC BD
A C
B
Ejercicios
B) El valor de los ángulos opuestos por el vértice, indicados es:
D
A 2X+15 AD=1350 , 1150, 1250 o 1450
X X= 550, 650, 450 o 350
B
C
C) De la siguiente gráfica encontrar el valor de X y Y, en las siguientes respuestas:
S X= 500, 600, 200, 400 o 300
A 2X B Y= 200, 300, 450, 500 o 600
3X-20
C D
Y+10
S’

17. D) Determina en las respuestas el suplemento y complemento del ángulo 890 59’ 60’’
complemento suplemento
a) 420 25’ 37’’ a) 1040 03’ 43’’
b) 440 28’ 39’’ b) 1060 07’ 45’’
c) 410 25’ 37’’ c) 1050 03’ 43’
d) 430 28’ 39’’ d) 1070 07’45’’
F) Coloca los valores de los ángulos que se piden de la siguiente lista:
a c ∠a = a) 1000
∠c = b) 1300
∠s = c) 500
∠y = d) 500
y x= 800 s m ∠m = e) 800
C.- Encontrar el valor de X y Y
B
3x+y x+y2
x+y+5 20-x
A 3x 3y C
3y+5 6y-x2
D
E.- Encontrar el valor de x.
X+100
x
C) Encontrar el valor de X y Y de la siguiente lista de valores:
D ∆I = ∆II, los lados correspondien
I tes son iguales;
A Y-5 260 C
420 X+ 200
VALORES
II
B X= 12, 6, 16, 7 o 18
Y= 47, 27, 37 o 17

18. D) Una escalera de 15 m está recargada en un edificio a la altura de un anuncio; una
plomada de 2 m de largo pende de la escalera y toca el piso a una distancia de 250 cm
del pie de la escalera. En la lista de valores encuentra la altura a que se encuentra el
anuncio.
A = 13.5m, 6.37m, 12.5m o 7.37m
x 15m
2m
250 cm
E) Encontrar el ángulo WUV
W
∠ WUV= 450, 600, 750, 500 o 350
1000 U
V
F) Encontrar el valor del ángulo BTC en la siguiente lista de ángulos:
T
A B
Si AB ⊥ al diámetro TD y TC
∠=50 , 45 , 90 o 75
0 0 0 0
es una cuerda. TC = 1000
C Hallar el ∠ BTC =
D
G) Teorema de la proporcionalidad: determinar la medida de X en la siguiente lista de
valores y asigna los resultados a los lados cuyo valor se desconoce:
C X= 10, 9, 17, 16 o 15
X 5 12
D E
X+4
A B

19. H) Encontrar la longitud del segmento X de la lista de valores, de las siguientes figuras:
12
X = 10, 12, 14 o 15
13 x 13
22
X = 4, 6, 8 o 2
√ 193 3x
2x-1
RESPUESTAS DE LA UNIDAD Nº 1
A) 1.- (5), 2.- (4), 3.- (3), 4.- (1), 5.- (2)
B) AD=1250 y X=550
C) X=200 y Y=300
D) Complemento = 410 25’ 37’’ Suplemento = 1040 03’ 43’’
E) a) < 900 , b) 900 , c) >900 pero < 1800 , d) 1800 , e) >1800 pero < 3600 , f) 3600
F) ∠a = 800, ∠c = 500, ∠s = 500, ∠y = 1000, ∠m = 1300
G) a) Mediana y baricentro, b) Circuncentro y mediatriz, c) Incentro y bisectriz, d)
ortocentro y altura, e) Altura, altura, altura y ortocentro, f) Recta de Euler-ortocentro,
baricentro y circuncentro.
RESPUESTAS DE LA UNIDAD Nº 2
A) a) l.a.l. = l.a.l.
B) c) l.l.l. = l.l.l.
C) X = 6 y Y = 47
D) Trazo
E) Traslado
F) Rotación
G) a) (V), b) (F), c) (V), d) (V), e) (F), f) (V)

20. RESPUESTAS DE LA UNIDAD Nº 3
A) Medir y construir
B) AB = 85.3 mm, AC = 69.3 mm, BC = 58.6 mm
C) ∠A, ∠C, ∠E, proporción = 1/3
D) X= 7.37 m
E) ∠WUV = 500
F) ∠WUV = 500
G) X = 10
H) a) X= 12, X = 4
SEMEJANZA Y CÍRCULO
Semejanza
Si vemos dos mapas de un país, a escalas distintas, decimos que son
semejantes; dos reproducciones a tamaños distintos de una misma fotografía son
semejantes.
Si dos figuras son semejantes llamamos partes homólogas a aquella parte de
una de las figuras y su imagen bajo la semejanza. Así, un segmento se transforma bajo
la semejanza en otro segmento, les llamaremos segmentos homólogos; a un vértice y
su imagen les llamaremos vértices homólogos.
.
Polígonos semejantes
Los polígonos que tienen la misma forma y diferentes dimensiones reciben el
nombre de polígonos semejantes.
En los polígono semejantes, los ángulos correspondientes son respectivamente
iguales y los lados homólogos son proporcionales, A estas dos características de los
polígonos semejantes se les llama condiciones de semejanza.
En los polígonos semejantes: ABCDE y A’B’C’D’E’ se tiene:
D
D’
C C’ a) ∠A = ∠A’,∠B = ∠B’, ∠C = ∠C’
E E’ ∠D = ∠D’ y ∠E = ∠E’ además:
A B A’ B’
b) AB/A’B’ = BC/B’C’ = CD/C’D’ = DE/D’E’ = EA/E’A’
Los triángulos equiláteros, los cuadrados y los círculos por sus propias
características de construcción, resultan ser siempre figuras semejantes entre sí; es
decir:
 Todos los triángulos equiláteros son semejantes.
 Todos los cuadrados son semejantes.

21.  Todos los círculos son semejantes.
Teorema de Pitágoras
En un triángulo rectángulo el cuadrado construido sobre la hipotenusa es igual a
la suma de los cuadrados construidos sobre los catetos.
Este teorema es de gran importancia debido a sus múltiples aplicaciones en los
problemas en que se trata del cálculo de un cateto o bien del cálculo de la hipotenusa
en los triángulos rectángulos
c2
a2 c
a
b
b2
c2 = a2 + b2 está expresando algebraicamente el enunciado del problema. De esta
fórmula, despejando c, a y b se pueden deducir tres fórmulas que nos den los valores
de la hipotenusa y los catetos:
c2 = a2 + b2 ∴ c = √a2 + b2
a = √c2 - b2
b = √c2 - a2
Ejemplos y soluciones
Dado el triángulo rectángulo ABC, hallar la medida del lado cuyo valor se
desconoce.
B 1.- a=5, b=12, c=?
2.- a=8, c=17, b=?
c a 3.- b=8, c=10, a=?
A b C

22. 1.- c = √a2 + b2 = √52 + 122 = √25 + 144 = √ 169 = 13
2.- b = √c2 - a2 = √172 - 82 = √284 - 64 = √ 225 = 15
3.- a = √c2 - b2 = √102 - 82 = √100 - 64 = √ 36 = 6
Con base en los datos de la figura, calcular los valores de x y z
B
En el ∆ ABC En el ∆ BCD
17 (9+X)2+82 =172 X2+82 = Z2
8 81+18X+X2+64 = 289 62+82 = Z2
Z X2+18X-144 = 0 36+64 = Z2
A C (X+24)(X-6) = 0 100 = Z2
9 D X X1 = -24 √100
X2 = 6 Z = 10
Se elimina el valor de x = -24 ya que x representa la medida de un segmento
Circunferencia y círculo
Se llama circunferencia al conjunto de todos los puntos del plan que equidistan de otro
punto llamado centro.
Se llama círculo al conjunto de los puntos interiores a la circunferencia.
r
r
Circunferencia Círculo
Líneas notables
A B AB cuerda
I CD diámetro
C O D EF secante
GH tangente
E F OI radio
G P H
Cuerda: Segmento de recta que une dos puntos de la circunferencia.
Diámetro: Es la cuerda que pasa por el centro de la circunferencia.
Secante: Es la recta que corta a la circunferencia en dos puntos.

23. Tangente: Es la recta que toca a la circunferencia en un punto.
Radio: Es el segmento de recta que une el centro de la circunferencia con un punto
cualquiera de la misma.
C
∩
AC arco AC
A B ∩
O
BC arco BC
∩
ACB arco ACB
Semicircunferencia ∩ Semicírculo
CAB arco CAB
Arco: Es una parte de la circunferencia
Semicircunferencia: Es un arco de longitud igual a la mitad de la circunferencia.
Arco mayor: Es aquel que mide más que una semicircunferencia.
Arco menor: Es aquel que mide menos que una semicircunferencia.
Ángulos notables
B A B D A
C C
E
o
A
A C D B
Ángulo central Ángulo inscrito Ángulo interior Ángulo externo
Ángulo central: Es aquel que está formado por dos radios. El ∠AOB intercepta o
subtiende al AB o a la cuerda AB, también se dice que el arco AB está comprendido
entre los lados del ángulo.
Ángulo inscrito: Es aquel que stá formado por dos cuerdas y tiene su vértice sobre la
circunferencia.
Ángulo interiror: Es aquel que está formado por dos cuerdas que se cortan.
Ángulo exteriror:Es aquel que está formado por dos secantes que se cortan en un punto
fuera del círculo.

24. MEDICIÓN DE LOS ÁNGULOS EN LA CIRCUNFERENCIA
CLASE DE ÁNGULO FIGURA FÓRMULA
B
Ángulo central C = AB
O C
B C
Inscrito B = ½ AC
A
B C
a 0
∠B = ½ AB
Semi-inscrito ∠B = ½a0
A
E D
Interior B = ½ (AC+ED)
A C
B B
D
Formado por dos secantes A A = ½ (BC-DE)
C E
A B
Po una secante y una 0 A = ½ (BC-BD)
taangente D b0 ab a0
0
a0 A = ½ (a0- b0)
B
C
B
A
Por dos tangentes C A = ½ (BDC-BC)
D
Ejemplos y soluciones
Si y = 40º, hallar ∠x
D
C X A ∠x = BC-DE = 100º- 40º = 30º
Y 2 2
100º E
B

25. AC =40º
C BD = 70º
A hallar ∠AEC
B
D
Encontrar x así como y t y t’ son tangentes
P
t
y
x
140º
t’
Q
RESUELVE LOS SIGUIENTE EJERCICIOS
1.- Un triángulo tiene una base de 10 cm y una altura de 8 cm cuánto mide el lado del
cuadrado que tiene una área igual a la del triángulo.
3.- Encontrar el área del cuadrado mayor y del cuadrado menor en la siguiente figura:
b h
h
b
b
h
h b
5.- Encontrar el valor de X sabiendo que el área sombreada de la figura es de 9 cm.
x
4m x
6m

26. RESUELVA LOS SIGUIENTES EJERCICIOS
1.- Encuentra le valor de los ángulos X y Y en los siguientes triángulos
C C
65º 4X
30º
y x 40º 2X 3X
A B D A B
2.- ¿Cuál es el valor de los ángulos opuestos por el vértice indicados
A D C
A
2x +15 S
x+y
x x-2y
150º
S’
C B
D
B
4.- Encontrar el valor de X y Y
D A B
I
50º
A Y-5 260 C D E
20º Y
420 X+ 200
X

27. 6.- En las siguientes figuras congruentes encontrar el valor de X y Y
x+8 D E 3x
A B C B
I II
4y x-6º
3y-5 2x+7
3y+6º
x
C A B
1.- Encontrar los valores de los ángulos X y Y de las siguientes figuras.
A B
55º C D
20º
Y
X
E F
3.- ¿Cuál es el valor de los ángulos opuestos por el vértice indicados
A D C
A
2x +15 S
x+y
x x-2y
150º
S’
C B
D
B

28. 5.- Un jardín tiene la forma de cuadrado de 8 m de lado, lo atraviezan dos pasillos
perpendiculares del mismo ancho X. Encontrar X si se sabe que se debe pavimentar
39 m2
X
8m
X
8m
Ejemplos y soluciones:
Calcular el área de una ventana triangular con las siguientes medidas.
A = ½ ba = ½ (5m) (6m) = 15 m2
5m A = 15 m2
6m
Calcular el área de un triángulo cuyos lados miden 85 mm, 47 mm, y 62 mm de longitud
S = 85 + 47 + 62 = 97 mm A= √ 97 (97-85) (97-47) (97-62) = 1427 mm2
2
A = 1427 mm2