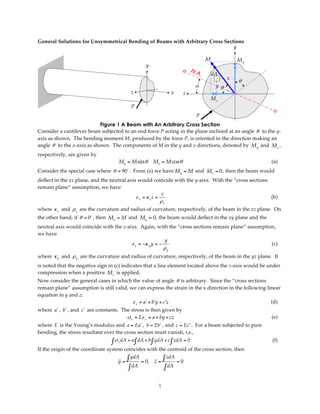
1. General Solutions for Unsymmetrical Bending of Beams with Arbitrary Cross Sections
y
M My
y
dA
z
θ
α yθ
z x z
Mz
P
P
Figure 1 A Beam with An Arbitrary Cross Section
Consider a cantilever beam subjected to an end force P acting in the plane inclined at an angle θ to the y-­‐‑
axis as shown. The bending moment M, produced by the force P, is oriented in the direction making an
angle θ to the z-­‐‑axis as shown. The components of M in the y and z-­‐‑directions, denoted by M y and M z ,
respectively, are given by
My = M sinθ Mz = M cosθ (a)
Consider the special case where θ = 90 . From (a) we have My = M and Mz = 0 , then the beam would

deflect in the xz plane, and the neutral axis would coincide with the y-­‐‑aixs. With the “cross sections
remain plane” assumption, we have
z
ε x = κ z z = (b)
ρz
where κ z and ρ z are the curvature and radius of curvature, respectively, of the beam in the xz plane. On
the other hand, if θ = 0 , then Mz = M and My = 0 , the beam would deflect in the xy plane and the
neutral axis would coincide with the z-­‐‑aixs. Again, with the “cross sections remain plane” assumption,
we have
y
ε x = −κ y y = − (c)
ρy
where κ y and ρ y are the curvature and radius of curvature, respectively, of the beam in the yz plane. It
is noted that the negative sign in (c) indicates that a line element located above the z-­‐‑axis would be under
compression when a positive M z is applied.
Now consider the general cases in which the value of angle θ is arbitrary. Since the “cross sections
remain plane” assumption is still valid, we can express the strain in the x direction in the following linear
equation in y and z:
ε x = aʹ′ + bʹ′y + cʹ′z (d)
where aʹ′ , bʹ′ , and cʹ′ are constants. The stress is then given by
σ x = Eε x = a + by + cz (e)
where E is the Young’s modulus and a = Eaʹ′ , b = Ebʹ′ , and c = Ec ʹ′ . For a beam subjected to pure
bending, the stress resultant over the cross section must vanish, i.e.,
∫ σ x dA = a ∫ dA + b∫ ydA + c ∫ zdA = 0 (f)
If the origin of the coordinate system coincides with the centroid of the cross section, then
y=
∫ ydA = 0, z=
∫ zdA = 0
∫ dA ∫ dA
1

2. Consequently, a = 0 and (e) becomes
σ x = by + cz (g)
The resultant moments on the cross section are given by
M y = ∫ σ x zdA = b ∫ yzdA + c ∫ z 2 dA = bI yz + cI y (h)
M z = − ∫ σ x ydA = −b ∫ y 2 dA − c ∫ yzdA = −bI z − cI yz (i)
where
I y = ∫ z 2 dA , I z = ∫ y 2 dA , I yz = ∫ yzdA
are the moments of inertia of the cross section. Solving (h) and (i) simultaneously yields
M z I y + M y I yz M y I z + M z I yz
b=− 2
, c= 2
(j)
I y I z − I yz I y I z − I yz
Substituting (j) into (g) gives
M z I y + M y I yz M y I z + M z I yz
σx = − 2
y+ 2
z (k)
IyIz − I yz I y I z − I yz
The neutral axis, by definition, is the line along which stress vanishes. Thus, by setting σ x = 0 in (k), we
have
y M y I z + M z I yz I yz + I z tan θ I z + I yz cot θ
tan α = = = = (l)
z M z I y + M y I yz I y + I yz tan θ I yz + I y cot θ
in which α (see Fig. 1) is the angle measured clockwise from the z-­‐‑axis to the neutral axis, and
My M
tan θ = , or cotθ = z (m)
Mz My
Combining (k) and (m) and eliminating M y , we obtain the following simplified equation in terms of M z
and angle α for calculating the stresses:
Mz (y − z tanα )
σx = − (n)
I z − I yz tan α
If the y-­‐‑ and z-­‐‑axes coincide with the principal axes, then I yz = 0 and (l) reduces to
Iz
tan α = tan θ
Iy
which is the same as (6-­‐‑19) in the textbook. Furthermore, if θ = 0 (i.e., Mz = M and My = 0 ), then α = 0
and (n) becomes
Mz y
σx = −
Iz
Example:
A 5.0 m long simply-­‐‑supported beam is subjected to a force P = 4 kN at a point that is 2.0 m away from
the far end, as shown in the figure. The dimensions of the L-­‐‑shaped cross section are shown in the figure.
If the force P is applied in an inclined plane making a 10° angle with the y-­‐‑axis, determine the locations
and magnitudes of the maximum tensile and compressive stresses in the beam.
Solution:
(a) Locate the centroid of the cross section (in terms of distances y 0 and z0 measured from point A):
(120 × 10)(60) + (70 × 10)(5 )
y0 = = 39.74 mm
(120 × 10) + (70 × 10)
(120 × 10)(5) + (70 × 10)(45)
z0 = = 19.74 mm
(120 × 10) + (70 × 10)
2

3. P y
10
B
10 mm
2 m P 120 mm
α
z M
10
10 mm
3 m y0
A
z0
80 mm
Figure 2 Umsymmetric Bending of A Simply-Supported Beam
(b) Determine the moments of inertia:
(120)(10)3 (10)(70)3
Iy = + (120)(10)(19.74 − 5)2 + + (10)(70)(45 − 19.74 )2 = 1.003 × 106 mm 4
12 12
(10)(120)3 (70)(10)3
Iz = + (10)(120)(60 − 39.74 )2 + + (70)(10)(39.74 − 5)2 = 2.783 × 106 mm 4
12 12
I yz = (10)(1120)(60 − 39.74 )(19.74 − 5) + (70)(10)(5 − 39.74)(19.74 − 45) = 0.973 × 106 mm 4
(c) Determine the neutral axis:
Since θ = −10 (i.e., positive θ measured clockwise from the z axis), we have, from (l),
I yz + I z tan θ 0.973 × 10 6 + 2.783 × 10 6 × tan − 10( )
tan α = = = 0.580
I y + I yz tan θ 1.003 × 10 6 + 0.973 × 10 6 × tan − 10( )
The neutral axis thus is oriented at the angle
α = tan−1 (0.580) = 0.526 rad = 30.12
(d) Determine the maximum stresses in the beam:
The maximum bending moment along the beam occurs at the point where the load P is applied, i.e.,
Pab (4.0 )(2.0)(3.0)
Mmax = = = 4.8 kN ⋅ m = 4.8 × 106 N ⋅ mm
L 5.0
where L = 5.0 m , a = 2.0 m , and b = 3.0 m . The y and z components of this moment are
My = Mmax sin θ = −0.834 × 106 N ⋅ mm
Mz = Mmax cos θ = 4.727 × 106 N ⋅ mm
From Fig.2 it is easy to see that the two locations denoted by A and B are the farthest from the neutral
axis, hence would experience the highest tensile or compressive stresses. The y and z coordinates of
those two points are A(−39.74 , 19.74 ) and B(80.26 , 9.74 ) , respectively. The maximum tensile stress,
occurs at point A, is given by
3

4. M z (y − z tan α )
σx = −
I z − I yz tan α
=−
(4.727 × 10 )[− 39.74 − (19.74)tan(30.12 )]
6 
2.783 × 10 − (0.973 × 10 )tan(30.12 )
6 6 
N
= 109.0 × 106
= 109.0 MPa
mm 2
The maximum compressive stress, occurs at point B, is given by
M (y − z tan α )
σx = − z
I z − I yz tan α
=−
(4.727 × 10 )[80.26 − (9.74)tan(30.12 )]
6 
2.783 × 10 − (0.973 × 10 )tan(30.12 )
6 6 
N
= −159.0 × 106 = −159.0 MPa
mm 2
(e) Solve the same problem by using the method outlined in Section 6-­‐‑5 of the textbook:
The principal axes are denoted as Y and Z, respectively, in Fig.3. The directions of the principal axes
and the principal moments of inertia of the cross section can be obtained by using (A-­‐‑11) and (A-­‐‑12)
in the textbook. Let β be the angle between the principal axis and y-­‐‑axis (see Fig.2), then from (A-­‐‑11)
2 I yz 2(0.973 × 106 )
tan 2θ p = tan 2 β = − =− = 1.093
Iy − Iz 1.003 × 10 6 − 2.783 × 10 6
and
1
β = tan −1 (1.093) = 23.8
2
The principal moments of inertia can be obtained by substituting the value of β in (A-­‐‑10), or using
(A-­‐‑12):
P y
Y
10
B
β
π
−β
2
ψ α
z M
10
β
Z
A
Figure 3 Neutral Axis and Principal Axes
4

5. 2
Iy + Iz ⎛ I y − I z ⎞ 2 6 4 6 4
I max,min = ⎜ 2 ⎟ + I yz = 3.212 × 10 mm , 0.574 × 10 mm ,
± ⎜ ⎟
2 ⎝ ⎠
Thus,
IY = 0.574 × 106 mm 4 I Z = 3.212 × 106 mm 4
The components of M in the Y and Z directions, respectively, are now given by
MY = M sin(β − 10 ) = 1.143 × 106 N ⋅ mm
MZ = M cos(β − 10 ) = 4.662 × 106 N ⋅ mm
The angle ψ , which determines the orientation of neutral axis and is measured clockwise from the Z-­‐‑
axis as shown in Fig.3, is given by
Y M I I
(
tan ψ = = Y Z = Z tan β − 10 = 1.374
Z MZ I Y I Y
)
from which
ψ = tan −1 (1.374 ) = 53.9
It can be seen from Fig.3 that
α = ψ − β = 30.1
which matches the value obtained previously. With respect to the principal axes, the stresses are
given by
M Z M Y
σ x = Y − Z
IY IZ
At point A, the coordinates are
YA = y A cos β + z A sin β = −28.4 mm
Z A = − y A sin β + z A cos β = 34.1 mm
and the stress is given by
MY Z MZY (1.143 × 10 3 )(34.1) (4.662 × 10 3 )(− 28.4 )
σx = − = − = 109.0 MPa
IY IZ 0.574 × 106 3.212 × 106
At point B, the coordinates are
YB = y B cos β + zB sin β = 77.4 mm
ZB = − y B sin β + zB cos β = −23.5 mm
and the stress is given by
M Z M Y (1.143 × 10 3 )(− 23.5 ) (4.662 × 10 3 )(77.4 )
σx = Y − Z = − = −159.0 MPa
IY IZ 0.574 × 106 3.212 × 106
5