Kalkulus modul viii turunan
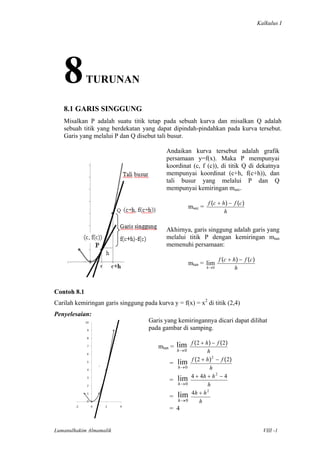
- 1. Kalkulus I 8 TURUNAN 8.1 GARIS SINGGUNG Misalkan P adalah suatu titik tetap pada sebuah kurva dan misalkan Q adalah sebuah titik yang berdekatan yang dapat dipindah-pindahkan pada kurva tersebut. Garis yang melalui P dan Q disebut tali busur. Andaikan kurva tersebut adalah grafik persamaan y=f(x). Maka P mempunyai koordinat (c, f (c)), di titik Q di dekatnya mempunyai koordinat (c+h, f(c+h)), dan tali busur yang melalui P dan Q mempunyai kemiringan msec. f (c + h) − f (c ) msec = h Akhirnya, garis singgung adalah garis yang melalui titik P dengan kemiringan mtan memenuhi persamaan: f (c + h) − f (c ) mtan = lim h →0 h Contoh 8.1 Carilah kemiringan garis singgung pada kurva y = f(x) = x2 di titik (2,4) Penyelesaian: Garis yang kemiringannya dicari dapat dilihat pada gambar di samping. lim f ( 2 + h ) − f ( 2) mtan = h→0 h f ( 2 + h ) 2 − f ( 2) = lim h→0 h 4 + 4h + h 2 − 4 = lim h→0 h 2 lim 4h + h = h→0 h = 4 Lumanulhakim Almamalik VIII -1
- 2. Kalkulus I Contoh 8.2 Jika f(x) = x2 – 3x + 2, tentukan persamaan garis singgung pada grafik f(x) di titik koordinat (3,2) Penyelesaian: lim {( x + h ) 2 - 3(x + h) + 2 } - ( x 2 − 3 x + 2) mtan = h→0 h = lim h →0 2 xh + h 2 - 3h = lim h→0 h = lim 2 x + h - 3 h→0 = 2x + 3 Gradien garis singgung di titik (3,2) adalah mtan (3) = 2.3–3 = 3 Jadi persamaan garis singgungnya adalah : y – 2 = 3 (x – 3 ) y = 3x – 7 atau 3x – y – 7 = 0 Latihan 1. Carilah persamaan garis singgung pada kurva y = 1/(2x) di titik (½, 1). 2. Carilah kemiringan garis singgung pada kurva y = x3 – 3x +2 di titik-titik dengan x = -2; 1,5 ; 3. 8.2 TURUNAN Turunan fungsi f adalah fungsi lain f′ (dibaca “f aksen”) yang nilainya pada sembarang bilangan c adalah f (c + h) − f (c ) f′ (c) = lim h →0 h asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan f terdiferensialkan di c. Jika f ’(c) ada, maka f kontinyu di c. Contoh 8.3 Jika f (x) = 13x - 6, tentukan f′ (4) Penyelesaian: f ( 4 + h ) − f ( 4) [13( 4 + h ) − 6] − [13( 4) − 6] f′ (4) = lim = lim h →0 h h →0 h Lumanulhakim Almamalik VIII -2
- 3. Kalkulus I 13h = lim = lim 13 = 0 h →0 h h →0 Contoh 8.4 Jika f(x) = x3 +7x, tentukan f ′(c) Penyelesaian: f (c + h) − f (c ) [(c + h )3 + 7(c + h )] − [c 3 + 7c] f ′(c) = lim = lim h →0 h h →0 h 3c 2 h + 3ch 2 + h 3 + 7 h = lim h →0 h = lim 3c 2 + 3ch + h 2 + 7 = 3c2 + 7 h →0 Contoh 8.5 Tentukan turunan dari fungsi f(x) = |x| Penyelesaian: Kita tahu bahwa Limit Kiri Limit Kanan Untuk y = f ( x) , cara penulisan di bawah ini semuanya digunakan untuk meng- ungkapkan turunan: dy d D(f), f '( x), y ', , [ f ( x)] dx dx Lumanulhakim Almamalik VIII -3
- 4. Kalkulus I Misalkan C, a, dan n adalah bilangan real dengan a> 0. Fungsi f(x) dan g(x) adalah fungsi-fungsi yang dapat diturunkan (didiferensiasi). Aturan Contoh 1. Kaidah bilangan konstanta Jika y = C , maka y ' = 0 . Jika y= 5, maka y ' = 0 . 2. Kaidah Pangkat Jika y = x n , maka y ' = n ⋅ x n −1 . Jika y = x 7 , maka y ' = 7 x 6 . 3. Kaidah Perkalian dengan Konstanta Jika y = 7 x 2 , Jika y = C ⋅ f ( x) , maka y ' = C ⋅ f '( x) . maka y ' = 7 ⋅ 2 x 2−1 = 14 x . 4. Penjumlahan dan Pengurangan: Jika y = 3 x 4 − 7 x , Jika y = f ( x) ± g ( x) , maka y ' = 12 x3 − 7 . maka y ' = f '( x) ± g '( x) 5. Eksponensial bilangan natural Jika y = 3e x , maka y = 3e x . Jika y = e x , maka y ' = e x . x 6. Jika y = a x , maka y = a x ln a . Jika y = 3 , maka y = 3x ln 3 Jika y = 3 ⋅ ln x , maka 1 7. Jika y = ln x , maka y ' = . 1 3 x y' = 3⋅ = x x 1 1 8. Jika y =loga x , maka y ' = . Jika y = log 4 x , maka y ' = x ln a x ⋅ ln 4 Contoh 8.6 Cari turunan fungsi f(x) = 2 x4 Penyelesaian: f’(x) = 2 x3 Contoh 8.7 Jika f(x) = 2 x3 – 4 x2 + 3 x + 5, tentukan f ′(x) Penyelesaian: d d d d f ′(x) = (2 x3) – (4 x2)+ (3 x) + (5) dx dx dx dx = 2 (3x2) – 4 (2x) + 3 (1) + 0 = 6 x2 – 8 x + 3 Lumanulhakim Almamalik VIII -4
- 5. Kalkulus I Contoh 8.8 Jika f ( x) = 5 x3 + 7 x 2.5 − 3x + 1 , tentukan f ′(x) Penyelesaian: d d d d d [ f ( x)] = (5 x 3 ) + (7 x 2.5 ) − (3 x) + (1) dx dx dx dx dx d d d d =5 ⋅ ( x 3 ) + 7 ⋅ ( x 2.5 ) − 3 ⋅ ( x) + (1) dx dx dx dx = 5 ⋅ 3 ⋅ x 3−1 + 7 ⋅ 2.5 ⋅ x 2.5−1 − 3 ⋅ 1 ⋅ x1−1 + 0 = 15 x 2 + 17.5 x1.5 − 3 1 Contoh 8.9 Jika y = 3t 2 − + e2 , tentukan y’ 2t 2 Penyelesaian: 1 Ingat bahwa n = a−n . a 1 1 y = 3t 2 − 2 + e2 = 3t 2 − t −2 + e 2 2t 2 dy 1 = 3 ⋅ 2 ⋅ t 2 −1 − (−2)t −2−1 + 0 dx 2 1 = 6t + t −3 = 6t + 3 t 4 Contoh 8.10 Jika g ( x) = 5 5 x 2 − + 2 , tentukan g’ x Penyelesaian: n Ingat bahwa m a n = a m Kita ubah terlebih dahulu fungsi menjadi 4 g ( x) = 5 ⋅ 5 x 2 − + 2 x = 5 ⋅ x 5 − 4 x −1 + 2 2 2 2 g '( x) = 5 ⋅ x 5 −1 − 4 ⋅ ( −1) ⋅ x −1−1 + 0 5 2 4 = 2 x − 5 + 4 x −2 = 3 + 2 3 x5 x 2 4 = + 2 5 3 x x Contoh 8.11 Jika y = 5 ⋅ e x + 2 ⋅ 3x , tentukan y’ Penyelesaian: Catatan 2 ⋅ 3x ≠ 6 x y ' = 5 ⋅ e x + 2 ⋅ 3x ln 3 . Lumanulhakim Almamalik VIII -5
- 6. Kalkulus I Contoh 8.12 Jika y = 3 ⋅ ln x − 4 ⋅ log 4 x , tentukan y′ Penyelesaian: dy 1 1 3 4 = 3⋅ − 4⋅ = − dx x x ⋅ ln 4 x x ⋅ ln 4 Contoh 8.13 Jika y = 5ex dan g = 3ex + 2, tentukan y′ dan g′ dy = 5ex dx dg = 3ex dx Kaidah Perkalian Fungsi Jika f(x) dan g(x) keduanya dapat diturunkan, maka turunan dari f ( x) ⋅ g ( x) dapat dicari menggunakan kaidah Perkalian. Jika f '( x) dan g '( x) ada, dan y = f ( x) ⋅ g ( x) , maka berlaku y ' = f '( x) ⋅ g ( x) + f ( x) ⋅ g '( x) Contoh 8.14 Jika y = (2x3 - x) (x4 + 3x), tentukan y′. Penyelesaian : Misalkan f (x) = 2x3 – x f ′(x) = 6x2 – 1 g(x) = x4 + 3 x g′(x) = 4x3 + 3 y ' = f '( x) ⋅ g ( x) + f ( x) ⋅ g '( x) = (6x2–1) (x4+3x) + (2x3–x)(4x3+3) = (6x6 – x4 +18x3 - 3x)+(8x6 - 4x4+6x3 - 3x) = 14 x 6 – 5 x4 + 24 x3 – 6 x Cara kedua dikalikan dulu sehingga : y = (2x7– x5 + 6 x4 – 3x2) ′ y′= 14x6 – 5x4 + 24x3 – 6x Lumanulhakim Almamalik VIII -6
- 7. Kalkulus I Contoh 8.15 Jika y = x ln x , tentukan y′ Penyelesaian: y ' = f '( x) ⋅ g ( x) + f ( x) ⋅ g '( x) 1 = 1 ⋅ ln x + x ⋅ x = ln x + 1 Kaidah Pembagian Fungsi f ( x) Jika f(x) dan g(x) keduanya dapat diturunkan, maka turunan dari y = dapat g ( x) dicari menggunakan kaidah Pembagian. Jika f '( x) dan g '( x) ada, dan y = f ( x) ⋅ g ( x) , maka berlaku f ' ( x ).g ( x ) − f ( x ).g ' ( x ) y' = dimana g ( x) ≠ 0 g 2 ( x) ( 2 x2 + x ) Contoh 8.16 Tentukan y′, jika y = x3 + 3 Penyelesaian: Misalkan f(x) = 2x2 + x f ′(x) = 4x + 1 g(x) = x3 + 3 g′(x) = 3x2 f ' ( x ).g ( x ) − f ( x ).g ' ( x ) y' = g 2 ( x) ( 4 x + 1) ( x3 + 3) − (2 x 2 + x)(3x 2 ) y′ = ( x3 + 3)2 ( 4 x 4 + x 3 + 12 x + 3) − ( 6 x 4 + 3x 3 ) = ( x 3 + 3) 2 − 2 x 4 − 2 x 2 + 12 x + 3 = ( x 3 + 3) 2 x2 − 1 Contoh 8.17 Jika h( x) = , tentukan h′(x) x2 + 1 Penyelesaian: Misalkan f(x) = x2 – 1 maka f ′(x) = 2x, g(x) = x2 + 1, maka g′(x) = 2x Lumanulhakim Almamalik VIII -7
- 8. Kalkulus I f ' ( x ).g ( x ) − f ( x ).g ' ( x ) y' = g 2 ( x) f ' ( x ).g ( x ) − f ( x ).g ' ( x ) y' = g 2 ( x) 2 x.( x 2 + 1) − ( x 2 − 1).2 x y' = ( x 2 + 1) 2 2x3 + 2x − 2x3 + 2x y' = ( x 2 + 1) 2 4x y' = ( x + 1) 2 2 Latihan dy dy dy 1. y = x2, = 2. y = 2x3, = 3. y = 9x27, = dx dx dx du dφ x3 dΨ 4. u = 3m6, = 5. ϕ = 7λ, = 6. ψ = , = dm dλ 12 dx dp dy dp 7. p = -5q2, = 8. y = 3x2 + 2x + 7, = 9. p = 9m - 2m3, = dq dx dm dy λ10 dφ 10. y = mx + c, = 11. ϕ = 14λ2 - + λ3 + 3, = dx 5 dλ 5 dy 3 1 dy dy 12. y = , = 13. y = 2 − 3 , = 14. y = x, = x dx x 2x dx dx dy dy 15. y = 3 x2 , = 16. y = 1 / x , = dx dx 8.3 TURUNAN SINUS DAN KOSINUS dy Jika y = sin x, maka = cos x dx dy y = cos x, = - sin x dx dy 1 y = tan x, = dx cos2 x Contoh 8.18 Jika y = 3 sin x – 5 cos x, tentukan y′ Lumanulhakim Almamalik VIII -8
- 9. Kalkulus I Penyelesaian: y′ = 3 cos x + 5 sin x Latihan Carilah turunan dari persamaan-persamaan berikut 1. y = 4 sin x – 5 cos x 2. y = sinx . cos x 3. y = cot x 4. y = sin2x 1 5. y = sin x 8.4 ATURAN RANTAI D x y = D u y.D x u dy dy du = . dx du dx Cara Penulisan Leibniz Contoh 8.19 Jika y(x) = (3x2 + 5 x – 7)4 , tentukan y′(x) Penyelesaian: Misalkan u = 3x2 + 5 x – 7 maka y(u) = u4 du dy = (6 x + 5) = 4u3 dx du dy dy du = . dx du dx dy = 4u3 . (6x+5) dx dy = 4 (3x2 + 5 x – 7) . (6x+5) dx 2x + 1 dy Contoh 8.20 Jika y = , tentukan 1− x dx Lumanulhakim Almamalik VIII -9
- 10. Kalkulus I Penyelesaian: 2x + 1 Misalkan u = maka y= u = u1/2 1− x du 2 (1 − x) − (2 x + 1)(−1) dy 1 -1/2 = = u dx (1 − x) 2 du 2 dy dy du = . dx du dx 1 -1/2 2 (1 − x) − (2 x + 1)(−1) = u 2 (1 − x) 2 −1 / 2 1 ⎛ 2x + 1 ⎞ 3 = ⎜ ⎟ . 2 ⎝ 1− x ⎠ (1 − x) 2 Contoh 8.21 Jika f(x) = (2x3 – x) (x4 + 3x) , tentukan f ′(x) Penyelesaian: Ada dua cara, pertama dengan aturan hasil kali f ′(x) = (2x3 – x) ′ ( x4 + 3x) + (2x3 – x) (x4 + 3 x) ′ = (6x2 – 1) (x4 + 3x) + (2x3 – x) (4x3 + 3) = (6x6 – x4 + 18 x3 – 3 x ) + (8 x6 – 4 x4 + 6 x3 – 3 x) = 14 x 6 – 5 x4 + 24 x3 – 6 x atau dikalikan dulu sehingga : f ′(x) = (2x7 – x5 + 6 x4 – 3 x2)′ = 14 x 6 – 5 x4 + 24 x3 – 6 x ( 2 x2 + x ) Contoh 8.22 Tentukan f ′(x) , jika f(x) = x3 + 3 Penyelesaian : Dengan aturan pembagian di dapat : ( 2 x 2 + x )' ( x 3 + 3) − ( 2 x 2 + x )( x 3 + 3)' f ′(x) = ( x 3 + 3) 2 ( 4 x + 1 ) ( x 3 + 3) − ( 2 x 2 + x )(3x 2 ) = ( x 3 + 3) 2 Lumanulhakim Almamalik VIII -10
- 11. Kalkulus I ( 4 x 4 + x 3 + 12 x + 3) − ( 6 x 4 + 3x 3 ) = ( x 3 + 3) 2 − 2 x 4 − 2 x 2 + 12 x + 3 = ( x 3 + 3) 2 Latihan 1. y = (2 – x3)4 1 2. y(x) = (1 − x 2 ) 3. y = (2 – x3)4 4. y = x2 − 1 5. Jika f(x) = (x2 -1)2 ( x2 +1)2 tentukan f ′(x) x3 + 2 x 6. Jika f(x) = 2 tentukan f ′(x) x +1 8.5 TURUNAN TINGKAT TINGGI dy d Turunan Orde Pertama f ', y ', , [ f ( x)], D1 f ( x) dx dx d2y d2 Turunan Orde Kedua f '', y '', 2 , 2 [ f ( x)], D 2 f ( x) dx dx d3y d3 Turunan Orde Ketiga f ''', y ''', , [ f ( x)], D 3 f ( x) dx 3 dx 3 dny dn Turunan Orde ke- nth ( n ≥ 4 ) f (n) , y (n) , , [ f ( x)], D n f ( x) dx n dx n Asumsi y = f ( x) and f ', f '', f ''', ... f ( n ) ada. Lumanulhakim Almamalik VIII -11
- 12. Kalkulus I Contoh 8.23 f ( x) = x 4 − 2 x3 + 5 x 2 − 10 x + 8 , Cari f ′, f ′′, f ′′′, f ′′′′, f (5) Penyelesaian: f '( x) = 4 x3 − 6 x 2 + 10 x − 10 f ''( x) = 12 x 2 − 12 x + 10 f '''( x) = 24 x − 12 f (4) ( x) = 24 f (5) ( x) = 0 Contoh 8.24 1 Tentukan turunan ketiga dari : f(x) = x4 – 2 x2 + - x2/3 ; x ≠ 0 x Penyelesaian: Dengan aturan pangkat dan sifat aljabar dari turunan didapat : 1 2 f ′(x) = 4 x3 – 4 x - 2 - x- 1/3 x 3 2 2 f ′′(x) = 12 x2 – 4 + 3 + x- 4/3 x 9 6 8 - 7/3 dan akhirnya : f ′′′(x) = 24 x – 4 - x x 27 Latihan 1 1. Tentukan turunan ketiga dari f(x) = x+ untuk x > 0 x 2. Tentukan f ′′(x) jika f(x)= x(x – 1)(x + 2) d2y 3. Hitunglah dari xy + x – 2y –1 = 0 dx 2 8.6 KECEPATAN DAN PERCEPATAN • Sebuah objek bergerak sepanjang sebuah garis koordinat. Apabila s=f(t) menyatakan posisi suatu obyek yang bergerak sebagai fungsi waktu, maka kecepatan ditentukan oleh persamaan v = f′′(t), sedangkan percepatan objek tersebut diperoleh dari turunan kecepatan dv atau a = . dt Jadi a = v ′ = s ′′ = f ′′(t) Contoh 8.25 Jarak yang ditempuh suatu gerakan partikel mempunyai persamaan: s = 2 t3 - 4 t2 + t – 6. Tentukan kecepatan dan percepatan partikel itu pada saat t. Lumanulhakim Almamalik VIII -12
- 13. Kalkulus I Penyelesaian : Kecepatan partikel merupakan turunan pertama dari jarak, sedangkan percepatan partikel merupakan turunan kedua dari jarak. Dengan demikian maka Jarak partikel adalah s = 2 t3 - 4 t2 + t – 6. Kecepatan partikel adalah v = s ′ = 6 t2 – 8 t + 1 Percepatan partikel adalah a = v ′ = s ′′ = 12 t - 8 Latihan 1. Posisi suatu gerakan partikel adalah : s = 2 sin 3t - 3 cos 2t. Tentukan kecepatan dan percepatan partikel itu pada saat t. 8.7 PENDIFERENSIALAN IMPLISIT • Apabila suatu fungsi yang didefinisikan secara implisit tidak dapat dinyatakan secara eksplisit atau pernyataan eksplisitnya sangat sukar, maka untuk mencari turunannya dapat ditentukan dengan menggunakan teorema turunan untuk jumlah dan perkalian dua fungsi dan aturan berantai. Contoh 8.26 dy Tentukan dari persamaan berikut y5 + x3y + y = x2 – x +3 dx Penyelesaian: Turunan persamaan y5 + x3y + y = x2 – x +3 adalah dy dy dy 5 y4 + 3 x2 y + x3 + =2x–1 dx dx dx dy dx [ ] 5 y 4 + x 3 + 1 = 2 x – 1 + 3 x2 y dy 2 x − 1 + 3x 2 y = dx 5 y 4 + x3 + 1 Contoh 8.27 Penyelesaian: Lumanulhakim Almamalik VIII -13
- 14. Kalkulus I 8.8 DIFERENSIAL DAN HAMPIRAN DIFERENSIAL dy = f′ (x). dx f′ (x) = dy/dx Contoh 8. Carilah dy jika a. y = x b. y = x3 – 3x +1 c. y = x 2 + 3 d. y = sin (x4 – 3x2+11) e. y = sin2(2x2+2) HAMPIRAN ATAU TAKSIRAN f(x + ∆x)≈ f(x) + dy = f(x) + f′ (x) ∆x Contoh 8.28 Berapa nilai taksiran yang baik terhadap 4,6 menggunakan persamaan diferensial. Penyelesaian: Dari nilai 4,6 kita akan dekati dengan persamaan y = x. Jika nilai x berubah dari 4 ke 4,6, maka x akan berubah dari 4 = 2 ke 4 +dy (secara taksiran). 1 1 Sekarang kita memiliki bahwa dy = ½ x 2 . dx = dx 2 x Sedangkan di x = 4 dan dx = 0,6 mempunyai nilai 1 dy = .0,6 = 0,15 2 4 Jadi 4,6 ≈ 4 +dy = 2 + 0,15 = 2,15 Latihan 1. Berapa nilai taksiran dari 8,2 2. Berapa nilai taksiran dari 3,92 3. Berapa nilai taksiran dari 3 28,3 4. Berapa nilai taksiran dari 3 26,91 5. Berapa nilai taksiran dari (12,2)2 Lumanulhakim Almamalik VIII -14
